
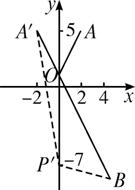
【探究】 先求出A点关于y轴的对称点A′(-2,5),直线A′B的方程:![]() ,化简为2x+y-1=0.
,化简为2x+y-1=0.
令x=0,得y=1.
故所求P点坐标为P(0,1).
【规律总结】 本题解法简单、易得,要掌握好,同时也要清楚这种解法的依据:
设P′是y轴上的异于P点的另一点,连P′A′、P′B,则有|P′A′|+|P′B|>?|A′B|?(三角形两边之和大于第三边),而|A′B|=|A′P|+?|PB|?=|PA|+|PB|.
∴|P′A′|+|P′B|>|PA|+|PB|,P点是使|PA|+|PB|取得最小值的点.
引申:本题若改为“在x轴上求一点P,使得|PA|+|PB|最小”,又如何求解.同学们自己完成.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:高中数学 来源:2011—2012学年浙江省海宁中学高二期中理科数学试卷 题型:解答题
如图,已知点A(2,3), B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
(Ⅰ)求AB边上的高CE所在直线的方程;
(Ⅱ)求△ABC的面积.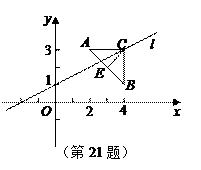
查看答案和解析>>
科目:高中数学 来源:2013届浙江省嘉兴市八校高二上期中联考理科数学试卷(解析版) 题型:解答题
(本题8分)如图,已知点A(2,3), B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
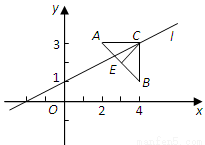
(Ⅰ)求AB边上的高CE所在直线的方程;
(Ⅱ)求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源:2013届浙江省高二期中理科数学试卷 题型:解答题
如图,已知点A(2,3), B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上.
(Ⅰ)求AB边上的高CE所在直线的方程;
(Ⅱ)求△ABC的面积.
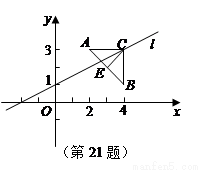
查看答案和解析>>
科目:高中数学 来源:2011-2012年山东省济宁市高二上学期期中考试文科数学 题型:解答题
(本题10分)如图,已知点A(2,3), B(4,1),△ABC是以AB为底边的等腰三角形,点C在直线l:x-2y+2=0上
(Ⅰ)求AB边上的高CE所在直线的方程
(Ⅱ)求△ABC的面积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com