
 a
a
 S△EBD•FC=
S△EBD•FC= S△EFD•h建立方程解之即可求出点B到平面FED的距离.
S△EFD•h建立方程解之即可求出点B到平面FED的距离.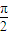 ,即BE⊥AC
,即BE⊥AC =
=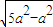 =2a
=2a BE•BD=
BE•BD=
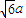

 FE•HEF=
FE•HEF= •
•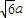 •
•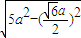 =
=
 S△EBD•FC=
S△EBD•FC= S△FED•h
S△FED•h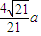



 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案科目:高中数学 来源: 题型:
 如图,弧AEC是半径为a的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FC⊥平面BED,FB=
如图,弧AEC是半径为a的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FC⊥平面BED,FB=| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 如图,弧AEC是半径为a的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FC⊥平面BDE,FB=
如图,弧AEC是半径为a的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,平面AEC外一点F满足FC⊥平面BDE,FB=| 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•浦东新区三模)如图,弧AEC是半径为r的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,线段ED与弧EC交于点G,且EG=
(2012•浦东新区三模)如图,弧AEC是半径为r的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,线段ED与弧EC交于点G,且EG=| 2 | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
 (2012•浦东新区三模)如图,弧AEC是半径为r的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,线段ED 与弧EC交于点G,且cos∠CBG=
(2012•浦东新区三模)如图,弧AEC是半径为r的半圆,AC为直径,点E为弧AC的中点,点B和点C为线段AD的三等分点,线段ED 与弧EC交于点G,且cos∠CBG=| 4 | 5 |
查看答案和解析>>
科目:高中数学 来源:浙江省期中题 题型:解答题
 。
。 
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com