
(本小题满分14分)已知数列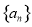 中,
中, ,其前
,其前 项和
项和 满足
满足 .
.
(Ⅰ)求证:数列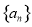 为等差数列,并求
为等差数列,并求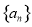 的通项公式;
的通项公式;
(Ⅱ)设 ,求数列
,求数列 的前
的前 项和
项和 ;
;
(Ⅲ)设 (
( 为非零整数,
为非零整数, ),是否存在确定
),是否存在确定 的值,使得对任意
的值,使得对任意 ,有
,有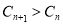 恒成立.若存在求出
恒成立.若存在求出 的值,若不存在说明理由。
的值,若不存在说明理由。
(Ⅰ)证明见解析,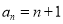 ;(Ⅱ)
;(Ⅱ)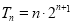 ;(Ⅲ)λ=﹣1;
;(Ⅲ)λ=﹣1;
【解析】
试题分析:1.错位相减法求和的方法为::设等差数列{an}的公差为d,等比数列{bn}的公比为q(q≠1)设Sn=a1b1+a2b2+ +anbn①,则qSn=a1b2+a2b3+ +an-1bn+anbn+1②,
①-②得:(1-q)Sn=a1b2+d(b2+ +bn)-anbn+1,进而转化为等比数列求和的问题.
错位相减法是数列求和的一种重要方法,是高考中的热点问题,值得注意的是,这种方法运算过程复杂,运算量大,应加强对解题过程的训练,重视运算能力的培养.
试题解析:
(Ⅰ)证明:由已知,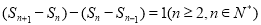 ,
,
即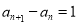 (n≥2,n∈N*),且
(n≥2,n∈N*),且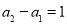 .
.
∴数列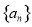 是以
是以 为首项,公差为1的等差数列,
为首项,公差为1的等差数列,
∴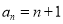 . (3分)
. (3分)
(Ⅱ)【解析】
由(Ⅰ)知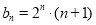 , 4分
, 4分
设它的前n项和为
∴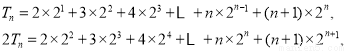
两式相减可得: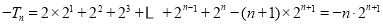
所以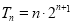 7分
7分
(Ⅲ)【解析】
∵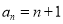 ,∴
,∴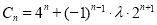 , 8分
, 8分
要使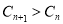 恒成立,则
恒成立,则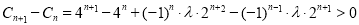 恒成立
恒成立
∴ 恒成立,
恒成立,
∴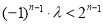 恒成立. 10分
恒成立. 10分
(ⅰ)当n为奇数时,即λ< 恒成立,当且仅当n=1时,
恒成立,当且仅当n=1时, 有最小值为1,∴λ<1.
有最小值为1,∴λ<1.
(ⅱ)当n为偶数时,即λ>﹣ 恒成立,当且仅当n=2时,﹣
恒成立,当且仅当n=2时,﹣ 有最大值
有最大值
﹣2,∴λ>﹣2.即﹣2<λ<1,又λ为非零整数,则λ=﹣1.
综上所述,存在λ=﹣1,使得对任意n∈N*,都有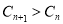 . 14分
. 14分
考点:等差数列定义、通项、数列求和等综合应用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:2014-2015学年山西省高二上学期期中考试文科数学试卷(解析版) 题型:选择题
在下列关于点P,直线 、
、 与平面
与平面 、
、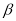 的命题中,正确的是
的命题中,正确的是
A.若 ,
, ,则
,则 ∥
∥
B.若 、
、 是异面直线,
是异面直线,

 ,
,  ∥
∥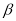 ,
, 

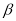 ,
,  ∥
∥ ,则
,则 ∥
∥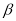 .
.
C.若 ,
, ,
, ,且
,且 ,则
,则
D.若 且
且 ,
, ,则
,则
查看答案和解析>>
科目:高中数学 来源:2014-2015学年山东省潍坊三县市高二上学期联考数学试卷(解析版) 题型:解答题
(本小题满分12分)如图,山脚下有一小塔AB,在塔底B测得山顶C的仰角为60°,在山顶C测得塔顶A的俯角为45°,已知塔高AB=20 m,求山高CD.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com