
分析 (1)根据不等式的左边减去右边化简结果为 (ad-bc)2≥0,可得不等式成立;
(2)从不等式的左边入手,左边对应的代数式的二倍,分别写成两两相加的形式,在三组相加的式子中分别用均值不等式,整理成最简形式,得到右边的2倍,两边同时除以2,得到结果.
解答 证明:∵(a2+b2)(c2+d2)-(ac+bd)2=( a2c2+a2d2+b2c2+b2d2)-(a2c2+2abcd+b2d2)
=(ad-bc)2≥0,
∴(a2+b2)(c2+d2)≥(ac+bd)2 成立;
(2)a2+b2+c2
=$\frac{1}{2}$(a2+b2+c2+a2+b2+c2)
≥$\frac{1}{2}$(2ab+2ca+2bc)=ab+bc+ca.
∴a2+b2+c2≥ab+bc+ca.
点评 本题主要考查用比较法证明不等式,考查均值不等式的应用,考查不等式的证明方法,把差变为因式乘积的形式,是解题的关键,属于中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 5 | B. | 6 | C. | 2$\sqrt{7}$ | D. | 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
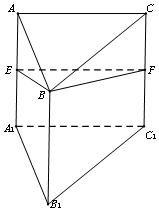 三棱柱ABC-A1B1C1的侧面AA1C1C为正方形,侧面AA1B1B⊥侧面BB1C1C,且AC=2,AB=$\sqrt{2}$,∠A1AB=45°,E、F分别为AA1、CC1的中点.
三棱柱ABC-A1B1C1的侧面AA1C1C为正方形,侧面AA1B1B⊥侧面BB1C1C,且AC=2,AB=$\sqrt{2}$,∠A1AB=45°,E、F分别为AA1、CC1的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (3,-4) | B. | (-4,3) | C. | (4,-3) | D. | (-3,-4) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com