
分析 首先判断函数定义域;然后根据题意函数f(x)=x2+lnx-2mx在定义域内是增函数即等价转化为:在x>0上恒有f'(x)≥0成立.
解答 解:由题意知函数f(x)的定义域为(0,+∞);
函数f(x)=x2+lnx-2mx在定义域内是增函数即等价转化为:在x>0上恒有f'(x)≥0成立.
f'(x)=2x+$\frac{1}{x}$-2m≥0⇒2x+$\frac{1}{x}$≥2m,而2x+$\frac{1}{x}$≥2$\sqrt{2}$,当且仅当x=$\frac{\sqrt{2}}{2}$时取等号;
∴2m≤2$\sqrt{2}$⇒m≤$\sqrt{2}$
故答案为:[$\sqrt{2}$,+∞)
点评 本题主要考查了函数单调性与导数的关系,以及基本不等式应用,属常规题型,考生应熟练掌握.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆Cl的方程为$\frac{{x}^{2}}{{4}^{2}}$+$\frac{{y}^{2}}{{3}^{2}}$=1,椭圆C2的短轴为C1的长轴且离心率为$\frac{\sqrt{3}}{2}$.
已知椭圆Cl的方程为$\frac{{x}^{2}}{{4}^{2}}$+$\frac{{y}^{2}}{{3}^{2}}$=1,椭圆C2的短轴为C1的长轴且离心率为$\frac{\sqrt{3}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
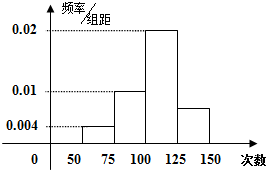 为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将所得的数据整理后,画频率分布直方图.已知图中横轴从左向右的分组为[50,75)、[75,100)、[100,125)、[125,150],纵轴前3个对应值分别为0.004、0.01、0.02,因失误第4个对应值丢失.
为了了解小学生的体能情况,抽取了某校一个年级的部分学生进行一分钟跳绳次数测试,将所得的数据整理后,画频率分布直方图.已知图中横轴从左向右的分组为[50,75)、[75,100)、[100,125)、[125,150],纵轴前3个对应值分别为0.004、0.01、0.02,因失误第4个对应值丢失.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com