


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
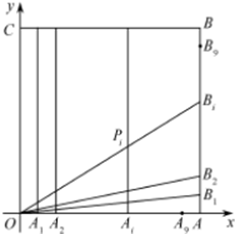 如图,在正方形OABC中,O为坐标原点,点A的坐标为(10,0),点C的坐标为(0,10),分别将线段OA和AB十等分,分点分别记为A1,A2,…,A9和B1,B2,…,B9,连接OBi,过Ai作x轴的垂线与OBi,交于点Pi(i∈N*,1≤i≤9).
如图,在正方形OABC中,O为坐标原点,点A的坐标为(10,0),点C的坐标为(0,10),分别将线段OA和AB十等分,分点分别记为A1,A2,…,A9和B1,B2,…,B9,连接OBi,过Ai作x轴的垂线与OBi,交于点Pi(i∈N*,1≤i≤9).| MC |
| CN |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
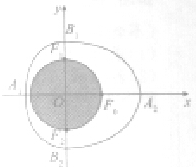 某服饰公司设计类一款服饰饰品,如图外面是红色透明水晶材质,里面是一个球形绿色玉质宝珠,其轴截面呦半椭圆C1:
某服饰公司设计类一款服饰饰品,如图外面是红色透明水晶材质,里面是一个球形绿色玉质宝珠,其轴截面呦半椭圆C1:| x2 |
| a2 |
| y2 |
| b2 |
| y2 |
| b2 |
| x2 |
| c2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 2 |
| ||
| 2 |
| ||
| 2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com