Question

函数y=|x²-2x-3|的单调递减区间是

 

．

Answer 1

考点：函数的单调性及单调区间

专题：函数的性质及应用

分析：利用二次函数的图象和性质化简绝对值，件即可单调函数的单调区间．

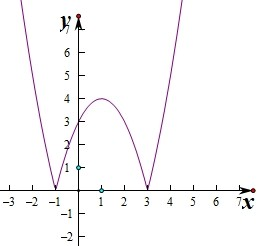
解答： 解：设t=x²-2x-3，
若x²-2x-3≥0，则x≥3或x≤-1，此时y=|x²-2x-3|=x²-2x-3，
若x²-2x-3＜0，则-1＜x＜3，此时y=|x²-2x-3|=-x²+2x+3，
作出函数的图象如图：
由图象可知，函数的单调递减区间为：
（-∞，-1）和（1，3）
故答案为：（-∞，-1）和（1，3）

点评：本题主要考查函数单调性和单调区间的求法，利用二次函数的图象和性质是解决本题的关键．