
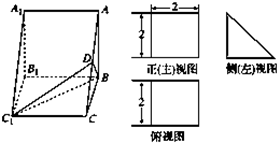
 直三棱柱ABC-A1B1C1的直观图及三视图如图所示,D为AC的中点,则下列命题是假命题的是( )
直三棱柱ABC-A1B1C1的直观图及三视图如图所示,D为AC的中点,则下列命题是假命题的是( )| A、AB1∥平面BDC1 | ||
| B、A1C⊥平面BDC1 | ||
| C、直三棱柱的体积V=4 | ||
D、直三棱柱的外接球的表面积为4
|
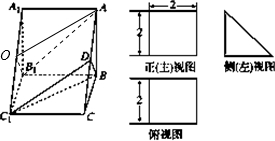 解:取A1C1中点O,连接OB1,AO,∵D为AC的中点,∴四边形DAOC1为平行四边形,
解:取A1C1中点O,连接OB1,AO,∵D为AC的中点,∴四边形DAOC1为平行四边形,| 1 |
| 2 |
| ||
| 2 |
| 3 |


 小天才课时作业系列答案
小天才课时作业系列答案 一课四练系列答案
一课四练系列答案 黄冈小状元满分冲刺微测验系列答案
黄冈小状元满分冲刺微测验系列答案 新辅教导学系列答案
新辅教导学系列答案科目:高中数学 来源: 题型:
 在2010年的人口普查中,某市人中普查办公室为召开普查工作意见反馈会,用分层抽样的方法,从某住宅小区中抽取A、B、C、D四个年龄段的居民共50人.如图是该小区这四个年龄段的人数条形图.
在2010年的人口普查中,某市人中普查办公室为召开普查工作意见反馈会,用分层抽样的方法,从某住宅小区中抽取A、B、C、D四个年龄段的居民共50人.如图是该小区这四个年龄段的人数条形图.查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com