
【题目】已知椭圆 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() 短轴两个端点为
短轴两个端点为 ![]() 且四边形
且四边形 ![]() 是边长为
是边长为 ![]() 的正方形.
的正方形.
(Ⅰ)求椭圆的方程;
(Ⅱ)若 ![]() 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点 ![]() 满足
满足 ![]() ,连接
,连接 ![]() ,交椭圆于点
,交椭圆于点 ![]() .证明:
.证明: ![]() 为定值.
为定值.
科目:高中数学 来源: 题型:
【题目】下列命题正确的是( )
A.存在 ![]() ,使得
,使得 ![]() 的否定是:不存在
的否定是:不存在 ![]() ,使得
,使得 ![]()
B.对任意 ![]() ,均有
,均有 ![]() 的否定是:存在
的否定是:存在 ![]() ,使得
,使得 ![]()
C.若 ![]() ,则
,则 ![]() 或
或 ![]() 的否命题是:若
的否命题是:若 ![]() ,则
,则 ![]() 或
或 ![]()
D.若 ![]() 为假命题,则命题
为假命题,则命题 ![]() 与
与 ![]() 必一真一假
必一真一假
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在 ![]() 上的函数
上的函数 ![]() 满足
满足 ![]() ,且
,且 ![]() 是偶函数,当
是偶函数,当 ![]() 时,
时, ![]() .令
.令 ![]() ,若在区间
,若在区间 ![]() 内,函数
内,函数 ![]() 有4个不相等实根,则实数
有4个不相等实根,则实数 ![]() 的取值范围是( )
的取值范围是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】根据国家环保部新修订的《环境空气质量标准》规定:居民区 ![]() 的年平均浓度不得超过3S微克/立方米,
的年平均浓度不得超过3S微克/立方米, ![]() 的24小时平均浓度不得超过75微克/立方米.某市环保局随机抽取了一居民区2016年20天
的24小时平均浓度不得超过75微克/立方米.某市环保局随机抽取了一居民区2016年20天 ![]() 的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如图表:
的24小时平均浓度(单位:微克/立方米)的监测数据,数据统计如图表:
组别 |
| 频数(天) | 频率 |
第一组 |
| 3 | 0.15 |
第二组 |
| 12 | 0.6 |
第三组 |
| 3 | 0.15 |
第四组 |
| 2 | 0.1 |
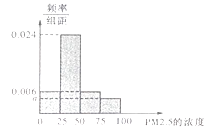
(Ⅰ)将这20天的测量结果按表中分组方法绘制成的样本频率分布直方图如图.
(ⅰ)求图中 ![]() 的值;
的值;
(ⅱ)在频率分布直方图中估算样本平均数,并根据样本估计总体的思想,从 ![]() 的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
的年平均浓度考虑,判断该居民区的环境质量是否需要改善?并说明理由.
(Ⅱ)将频率视为概率,对于2016年的某3天,记这3天中该居民区 ![]() 的24小时平均浓度符合环境空气质量标准的天数为
的24小时平均浓度符合环境空气质量标准的天数为 ![]() ,求
,求 ![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数 ![]() 的最小正周期为
的最小正周期为 ![]() ,将函数
,将函数 ![]() 的图象向左平移
的图象向左平移 ![]() 个单位长度,再向下平移
个单位长度,再向下平移 ![]() 个单位长度,得到函数
个单位长度,得到函数 ![]() 的图象.
的图象.
(Ⅰ)求函数 ![]() 的单调递增区间;
的单调递增区间;
(Ⅱ)在锐角 ![]() 中,角
中,角 ![]() 的对边分别为
的对边分别为 ![]() .若
.若 ![]() ,
, ![]() ,求
,求 ![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在矩形 ![]() 中,点
中,点 ![]() 在线段
在线段 ![]() 上,
上, ![]() ,
, ![]() ,沿直线
,沿直线 ![]() 将
将 ![]() 翻折成
翻折成 ![]() ,使点
,使点 ![]() 在平面
在平面 ![]() 上的射影
上的射影 ![]() 落在直线
落在直线 ![]() 上.
上.
(Ⅰ)求证:直线 ![]() 平面
平面 ![]() ;
;
(Ⅱ)求二面角 ![]() 的平面角的余弦值.
的平面角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)是定义域为R的周期函数,最小正周期为2,且f(1+x)=f(1-x),当-1≤x≤0时,f(x)=-x.
(1)判断f(x)的奇偶性;
(2)试求出函数f(x)在区间[-1,2]上的表达式.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com