
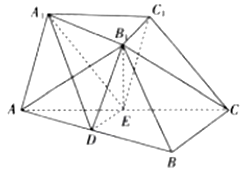
【题目】如图,在三棱台 ![]() 中,
中, ![]() ,
, ![]() 分别是
分别是 ![]() ,
, ![]() 的中点,
的中点, ![]() ,
, ![]() 平面
平面 ![]() ,且
,且 ![]() .
.
(1)证明: ![]() 平面
平面 ![]() ;
;
(2)若 ![]() ,
, ![]() 为等边三角形,求四棱锥
为等边三角形,求四棱锥 ![]() 的体积.
的体积.
【答案】
(1)解:设 ![]() 与
与 ![]() 相交于
相交于 ![]() ,连接
,连接 ![]() ,
,
由题意可知, ![]() ,
, ![]() ,
,
所以四边形 ![]() 是平行四边形,
是平行四边形,
从而 ![]() 是
是 ![]() 的中点.
的中点.
又 ![]() 是
是 ![]() 的中点,
的中点,
所以 ![]() .
.
又 ![]() 平面
平面 ![]() ,
, ![]() 平面
平面 ![]() ,
,
所以 ![]() 平面
平面 ![]()
(2)解:易证 ![]() ,
, ![]() 是三棱柱,
是三棱柱,
又因为 ![]() 平面
平面 ![]() ,所以
,所以 ![]() 是此三棱柱的高,
是此三棱柱的高,
同理 ![]() 也是三棱锥
也是三棱锥 ![]() 的高.
的高.
因为 ![]() ,
, ![]() 为等边三角形,
为等边三角形,
所以 ![]() ,
, ![]() ,
, ![]() ,
,
又 ![]() ,
,
所以 ![]() .
.
【解析】本题考查线面平行的证明,考查四棱锥的体积的求法.直线与平面平行的判定定理的实质是:对于平面外的一条直线,只需在平面内找到一条直线和这条直线平行,就可判定这条直线必和这个平面平行.即由线线平行得到线面平行.柱体、锥体、台体的体积公式:
V柱=sh,V锥=![]() Sh.
Sh.
【考点精析】本题主要考查了棱锥的结构特征和棱台的结构特征的相关知识点,需要掌握侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方;①上下底面是相似的平行多边形②侧面是梯形③侧棱交于原棱锥的顶点才能正确解答此题.


 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案科目:高中数学 来源: 题型:
【题目】我们可以用随机模拟的方法估计 ![]() 的值,如图程序框图表示其基本步骤(函数
的值,如图程序框图表示其基本步骤(函数 ![]() 是产生随机数的函数,它能随机产生
是产生随机数的函数,它能随机产生 ![]() 内的任何一个实数).若输出的结果为
内的任何一个实数).若输出的结果为 ![]() ,则由此可估计
,则由此可估计 ![]() 的近似值为( )
的近似值为( )
A.3.119
B.3.124
C.3.132
D.3.151
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】网店和实体店各有利弊,两者的结合将在未来一段时期内,成为商业的一个主要发展方向.某品牌行车记录仪支架销售公司从 ![]() 年
年 ![]() 月起开展网络销售与实体店体验安装结合的销售模式.根据几个月运营发现,产品的月销量
月起开展网络销售与实体店体验安装结合的销售模式.根据几个月运营发现,产品的月销量 ![]() 万件与投入实体店体验安装的费用
万件与投入实体店体验安装的费用 ![]() 万元之间满足
万元之间满足 ![]() 函数关系式.已知网店每月固定的各种费用支出为
函数关系式.已知网店每月固定的各种费用支出为 ![]() 万元,产品每
万元,产品每 ![]() 万件进货价格为
万件进货价格为 ![]() 万元,若每件产品的售价定为“进货价的
万元,若每件产品的售价定为“进货价的 ![]() ”与“平均每件产品的实体店体验安装费用的一半”之和,则该公司最大月利润是万元.
”与“平均每件产品的实体店体验安装费用的一半”之和,则该公司最大月利润是万元.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《九章算术》卷5《商功》记载一个问题“今有圆堡瑽,周四丈八尺,高一丈一尺 .问积几何?答曰:二千一百一十二尺.术曰:周自相乘,以高乘之,十二而一”.这里所说的圆堡瑽就是圆柱体,它的体积为“周自相乘,以高乘之,十二而一”. 就是说:圆堡瑽(圆柱体)的体积为 ![]() (底面圆的周长的平方
(底面圆的周长的平方 ![]() 高),则由此可推得圆周率
高),则由此可推得圆周率 ![]() 的取值为( )
的取值为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆 ![]() 的左、右焦点分别为
的左、右焦点分别为 ![]() 短轴两个端点为
短轴两个端点为 ![]() 且四边形
且四边形 ![]() 是边长为
是边长为 ![]() 的正方形.
的正方形.
(Ⅰ)求椭圆的方程;
(Ⅱ)若 ![]() 分别是椭圆长轴的左、右端点,动点
分别是椭圆长轴的左、右端点,动点 ![]() 满足
满足 ![]() ,连接
,连接 ![]() ,交椭圆于点
,交椭圆于点 ![]() .证明:
.证明: ![]() 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线 ![]() 的参数方程为
的参数方程为 ![]() (
( ![]() 为参数),直线
为参数),直线 ![]() 的参数方程为
的参数方程为  (
( ![]() 为参数).
为参数).
(Ⅰ)求曲线 ![]() 和直线
和直线 ![]() 的普通方程;
的普通方程;
(Ⅱ)若点 ![]() 为曲线
为曲线 ![]() 上一点,求点
上一点,求点 ![]() 到直线
到直线 ![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com