
【题目】已知数列![]() 都是由实数组成的无穷数列.
都是由实数组成的无穷数列.
(1)若![]() 都是等差数列,判断数列
都是等差数列,判断数列![]() 是否是等差数列,说明理由;
是否是等差数列,说明理由;
(2)若![]() ,且
,且![]() 是等比数列,求
是等比数列,求![]() 的所有可能值;
的所有可能值;
(3)若![]() 都是等差数列,数列
都是等差数列,数列![]() 满足
满足![]() ,求证:
,求证: ![]() 是等差数列的充要条件是:
是等差数列的充要条件是: ![]() 中至少有一个是常数.
中至少有一个是常数.
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前
的前![]() 项和为
项和为![]() ,对任意
,对任意![]() ,点
,点![]() 都在函数
都在函数![]() 的图象上.
的图象上.
(1)求![]() ,归纳数列
,归纳数列![]() 的通项公式(不必证明).
的通项公式(不必证明).
(2)将数列![]() 依次按
依次按![]() 项、
项、![]() 项、
项、![]() 项、
项、![]() 项、
项、![]() 项循环地分为
项循环地分为![]() ,
,![]()
![]() ,
,![]() ,
,![]() ,各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为
,各个括号内各数之和,设由这些和按原来括号的前后顺序构成的数列为![]() ,求
,求![]() 的值.
的值.
(3)设![]() 为数列
为数列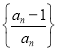 的前
的前![]() 项积,若不等式
项积,若不等式![]() 对一切
对一切![]() 都成立,其中
都成立,其中![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】
对定义在区间![]() 上的函数
上的函数![]() ,若存在闭区间
,若存在闭区间![]() 和常数
和常数![]() ,使得对任意的
,使得对任意的![]() 都有
都有![]() ,且对任意的
,且对任意的![]() 都有
都有![]() 恒成立,则称函数
恒成立,则称函数![]() 为区间
为区间![]() 上的“U型”函数。
上的“U型”函数。
(1)求证:函数![]() 是
是![]() 上的“U型”函数;
上的“U型”函数;
(2)设![]() 是(1)中的“U型”函数,若不等式
是(1)中的“U型”函数,若不等式![]() 对一切的
对一切的![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 是区间
是区间![]() 上的“U型”函数,求实数
上的“U型”函数,求实数![]() 和
和![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】记![]() 为数列
为数列![]() 的前
的前![]() 项和.“任意正整数
项和.“任意正整数![]() ,均有
,均有![]() ”是“
”是“![]() 为递增数列”的
为递增数列”的
A. 充分不必要条件 B. 必要不充分条件
C. 充要条件 D. 既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年6月25日,《固体废物污染环境防治法(修订草案)》初次提请全国人大常委会审议,草案对“生活垃圾污染环境的防治”进行了专章规定.草案提出,国家推行生活垃圾分类制度.为了了解人民群众对垃圾分类的认识,某市环保部门对该市市民进行了一次垃圾分类网络知识问卷调查,每一位市民仅有一次参加机会,通过随机抽样,得到参加问卷调查的1000人的得分(满分:100分)数据,统计结果如下表所示:
得分 |
|
|
|
|
|
|
|
频数 | 25 | 150 | 200 | 250 | 225 | 100 | 50 |
(1)由频数分布表可以认为,此次问卷调查的得分![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求
近似为这1000人得分的平均值(同一组数据用该组区间的中点值作为代表),请利用正态分布的知识求![]() ;
;
(2)在(1)的条件下,市环保部门为此次参加问卷调查的市民制定如下奖励方案:
①得分不低于![]() 的可以获赠2次随机话费,得分低于
的可以获赠2次随机话费,得分低于![]() 的可以获赠1次随机话费;
的可以获赠1次随机话费;
②每次获赠的随机话费和对应的概率为:
获赠的随机话费(单位:元) | 20 | 40 |
概率 |
|
|
现市民小王要参加此次问卷调查,记![]() (单位:元)为该市民参加问卷调查获赠的话费,求
(单位:元)为该市民参加问卷调查获赠的话费,求![]() 的分布列及数学期望.
的分布列及数学期望.
附:①![]() ;
;
②若![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 且
且![]() ,
,![]() 且
且![]() ,函数
,函数![]() .
.
(1)设![]() ,
,![]() ,若
,若![]() 是奇函数,求
是奇函数,求![]() 的值;
的值;
(2)设![]() ,
,![]() ,判断函数
,判断函数![]() 在
在![]() 上的单调性并加以证明;
上的单调性并加以证明;
(3)设![]() ,
,![]() ,
,![]() ,函数
,函数![]() 的图象是否关于某垂直于
的图象是否关于某垂直于![]() 轴的直线对称?如果是,求出该对称轴,如果不是,请说明理由.
轴的直线对称?如果是,求出该对称轴,如果不是,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com