
【题目】已知函数![]() (
(![]() 为自然对数的底数).
为自然对数的底数).
(1)讨论函数![]() 的单调性;
的单调性;
(2)当![]() 时,
时,![]() 恒成立,求整数
恒成立,求整数![]() 的最大值.
的最大值.
【答案】(1)见解析;(2) ![]() 的最大值为1.
的最大值为1.
【解析】
(1)根据![]() 的不同范围,判断导函数的符号,从而得到
的不同范围,判断导函数的符号,从而得到![]() 的单调性;(2)方法一:构造新函数
的单调性;(2)方法一:构造新函数![]() ,通过讨论
,通过讨论![]() 的范围,判断
的范围,判断![]() 单调性,从而确定结果;方法二:利用分离变量法,把问题变为
单调性,从而确定结果;方法二:利用分离变量法,把问题变为![]() ,求解函数最小值得到结果.
,求解函数最小值得到结果.
(1)![]()
![]()
当![]() 时,
时,![]()
![]() 在
在![]() 上递增;
上递增;
当![]() 时,令
时,令![]() ,解得:
,解得:![]()
![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
当![]() 时,
时,![]()
![]() 在
在![]() 上递减
上递减
(2)由题意得:![]()
即![]() 对于
对于![]() 恒成立
恒成立
方法一、令![]() ,则
,则![]()
当![]() 时,
时,![]()
![]() 在
在![]() 上递增,且
上递增,且![]() ,符合题意;
,符合题意;
当![]() 时,
时,![]()
![]() 时,
时,![]() 单调递增
单调递增
则存在![]() ,使得
,使得![]() ,且
,且![]() 在
在![]() 上递减,在
上递减,在![]() 上递增
上递增 ![]()
![]()
![]()
由![]() 得:
得:![]()
又![]()
![]() 整数
整数![]() 的最大值为
的最大值为![]()
另一方面,![]() 时,
时,![]() ,
,![]()
![]() ,
,![]()
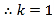 时成立
时成立
方法二、原不等式等价于:![]() 恒成立
恒成立
令![]()
![]()
令![]() ,则
,则![]()
![]() 在
在![]() 上递增,又
上递增,又![]() ,
,![]()
![]() 存在
存在![]() ,使得
,使得![]()
且![]() 在
在![]() 上递减,在
上递减,在![]() 上递增
上递增
![]()
又![]() ,
,![]()
![]()
![]()
又![]() ,整数
,整数![]() 的最大值为
的最大值为![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】有2012位学者参加某数学会议,他们中有些人相互认识,且满足:
(1)每个人至少认识其中的671个人;
(2)对于其中任意两个人![]() 、
、![]() ,若
,若![]() 、
、![]() 相互不认识,则总可以通过其他人间接认识,即存在
相互不认识,则总可以通过其他人间接认识,即存在![]() ,使得
,使得![]() 认识
认识![]() ,
,![]() 认识
认识![]() ,
,![]() 认识
认识![]() ;
;
(3)不可以将2012位学者排成一排,使得相邻的两个人相互认识.
证明:可以将2012位学者分成两组,其中一组能够排成一圈,使得相邻的人相互认识,另一组任何两个人不认识.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,抛物线
,抛物线![]() :
: ![]() 与抛物线
与抛物线![]() :
: ![]() 异于原点
异于原点![]() 的交点为
的交点为![]() ,且抛物线
,且抛物线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 在点
在点![]() 处的切线与
处的切线与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)若直线![]() 与抛物线
与抛物线![]() 交于点
交于点![]() ,
, ![]() ,且
,且![]() ,求
,求![]() ;
;
(2)证明: ![]() 的面积与四边形
的面积与四边形![]() 的面积之比为定值.
的面积之比为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙两地相距![]() ,汽车从甲地匀速行驶到乙地,速度不超过
,汽车从甲地匀速行驶到乙地,速度不超过![]() .已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度
.已知汽车每小时的运输成本(以元为单位)由可变部分和固定部分组成:可变部分与速度![]() (单位:
(单位:![]() )的平方成正比,且比例系数为
)的平方成正比,且比例系数为![]() ,固定部分为
,固定部分为![]() 元.
元.
(1)把全程运输成本![]() (元)表示为速度
(元)表示为速度![]() 的函数,并求出当
的函数,并求出当![]() ,
,![]() 时,汽车应以多大速度行驶,才能使得全程运输成本最小;
时,汽车应以多大速度行驶,才能使得全程运输成本最小;
(2)随着汽车的折旧,运输成本会发生一些变化,那么当![]() ,
,![]() 元,此时汽车的速度应调整为多大,才会使得运输成本最小.
元,此时汽车的速度应调整为多大,才会使得运输成本最小.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运动员每次射击命中不低于8环的概率为![]() ,命中8环以下的概率为
,命中8环以下的概率为![]() ,现用随机模拟的方法估计该运动员三次射击中有两次命中不低于8环,一次命中8环以下的概率:先用计算器产生0至9之间取整数值的随机数.指定0、1、2、3、4、5表示命中不低于8环,6、7、8、9表示命中8环以下,再以三个随机数作为一组.代表三次射击的结果,产生如下20组随机数:
,现用随机模拟的方法估计该运动员三次射击中有两次命中不低于8环,一次命中8环以下的概率:先用计算器产生0至9之间取整数值的随机数.指定0、1、2、3、4、5表示命中不低于8环,6、7、8、9表示命中8环以下,再以三个随机数作为一组.代表三次射击的结果,产生如下20组随机数:
524207443815510013429966027954
576086324409472796544917460962
据此估计,该运动员三次射击中有两次命中不低于8环,一次命中8环以下的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某大型电器企业,为了解组装车间职工的生活情况,从中随机抽取了![]() 名职工进行测试,得到频数分布表如下:
名职工进行测试,得到频数分布表如下:
日组装个数 |
|
|
|
|
|
|
人数 | 6 | 12 | 34 | 30 | 10 | 8 |
(1)现从参与测试的日组装个数少于![]() 的职工中任意选取
的职工中任意选取![]() 人,求至少有
人,求至少有![]() 人日组装个数少于
人日组装个数少于![]() 的概率;
的概率;
(2)由频数分布表可以认为,此次测试得到的日组装个数![]() 服从正态分布
服从正态分布![]() ,
,![]() 近似为这
近似为这![]() 人得分的平均值(同一组数据用该组区间的中点值作为代表).
人得分的平均值(同一组数据用该组区间的中点值作为代表).
(![]() 名职工,求日组装个数超过
名职工,求日组装个数超过![]() 的职工人数;
的职工人数;
(ii)为鼓励职工提高技能,企业决定对日组装个数超过![]() 的职工日工资增加
的职工日工资增加![]() 元,若在组装车间所有职工中任意选取
元,若在组装车间所有职工中任意选取![]() 人,求这三人增加的日工资总额的期望.
人,求这三人增加的日工资总额的期望.
附:若随机变量![]() 服从正态分布
服从正态分布![]() ,则
,则![]() ,
,![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)当a>0时,求函数f(x)的单调区间;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com