设函数
.
（1）设
，
，
，证明：
在区间
内存在唯一的零点；
（2）设
，若对任意
、
，有
，求
的取值范围.
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：高中数学 来源： 题型：解答题
学校操场边有一条小沟,沟沿是两条长150米的平行线段,沟宽
为2米,，与沟沿垂直的平面与沟的交线是一段抛物线，抛物线的顶点为
，对称轴与地面垂直，沟深2米，沟中水深1米．
（1）求水面宽；
（2）如图1所示形状的几何体称为柱体，已知柱体的体积为底面积乘以高，求沟中的水有多少立方米？
（3）现在学校要把这条水沟改挖(不准填土)成截面为等腰梯形的沟，使沟的底面与地面平行，沟深不变，两腰分别与抛物线相切（如图2），问改挖后的沟底宽为多少米时，所挖的土最少？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
甲厂以x千克/小时的速度运输生产某种产品(生产条件要求1≤x≤10)，每小时可获得利润是100(5x＋1－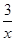
)元．
(1)要使生产该产品2小时获得的利润不低于3000元，求x的取值范围；
(2)要使生产900千克该产品获得的利润最大，问：甲厂应该选取何种生产速度？并求最大利润．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
如图，建立平面直角坐标系xOy，x轴在地平面上，y轴垂直于地平面，单位长度为1km，某炮位于坐标原点．已知炮弹发射后的轨迹在方程y＝kx－
(1＋k2)x2(k>0)表示的曲线上，其中k与发射方向有关．炮的射程是指炮弹落地点的横坐标．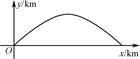
(1)求炮的最大射程；
(2)设在第一象限有一飞行物(忽略其大小)，其飞行高度为3.2km，试问它的横坐标a不超过多少时，炮弹可以击中它？请说明理由．
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
要制作一个如图的框架(单位：m)，要求所围成的总面积为19.5(m2)，其中ABCD是一个矩形，EFCD是一个等腰梯形，梯形高h＝
AB，tan∠FED＝
，设AB＝xm，BC＝ym.
(1)求y关于x的表达式；
(2)如何设计x、y的长度，才能使所用材料最少？
查看答案和解析>>
科目：高中数学 来源： 题型：解答题
有一种新型的洗衣液，去污速度特别快．已知每投放k(1≤k≤4，且k∈R)个单位的洗衣液在一定量水的洗衣机中，它在水中释放的浓度y(克/升)随着时间x(分钟)变化的函数关系式近似为y＝k·f(x)，其中f(x)＝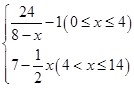
若多次投放，则某一时刻水中的洗衣液浓度为每次投放的洗衣液在相应时刻所释放的浓度之和．根据经验，当水中洗衣液的浓度不低于4(克/升)时，它才能起到有效去污的作用．
(1)若只投放一次k个单位的洗衣液，两分钟时水中洗衣液的浓度为3(克/升)，求k的值；
(2)若只投放一次4个单位的洗衣液，则有效去污时间可达几分钟？
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
.
在
上的最大值与最小值之差
”，对二次函数
，
，
在区间
时，
，
，
时，即
时，
，与题设矛盾！
，即
时，
恒成立；
，即
时，
.
为偶函数．
的值；
有且只有一个根，求实数
的取值范围．
满足
，当
时，
，且
.
的值；
的方程
有解，求
的取值范围.
命题
且命题
是
的必要条件，求实数m的取值范围