
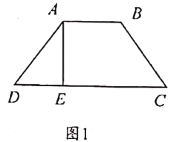
【题目】如图1,已知平面四边形![]() 中,
中,![]() .点
.点![]() 在
在![]() 上,且满足
上,且满足![]() .沿
.沿![]() 将
将![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() ,如图2.
,如图2.
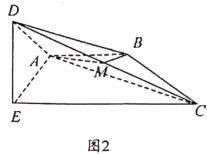
(1)若点![]() 是
是![]() 的中点,证明:
的中点,证明:![]() 平面
平面![]() ;
;
(2)在(1)的条件下,求三棱锥![]() 的体积.
的体积.
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是平行四边形,
是平行四边形,![]() 平面
平面![]() ,
,![]() 是棱
是棱![]() 上的一点,满足
上的一点,满足![]() 平面
平面![]() .
.
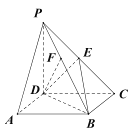
(Ⅰ)证明:![]() ;
;
(Ⅱ)设![]() ,
,![]() ,若
,若![]() 为棱
为棱![]() 上一点,使得直线
上一点,使得直线![]() 与平面
与平面![]() 所成角的大小为30°,求
所成角的大小为30°,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(Ⅰ)若![]() 的值域为
的值域为![]() ,求
,求![]() 的值;
的值;
(Ⅱ)巳![]() ,是否存在这祥的实数
,是否存在这祥的实数![]() ,使函数
,使函数![]() 在区间
在区间![]() 内有且只有一个零点.若存在,求出
内有且只有一个零点.若存在,求出![]() 的取值范围;若不存在,请说明理由.
的取值范围;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() ,其前
,其前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
⑴若![]() ,
,![]() ,
,![]() (
(![]() ),求证:数列
),求证:数列![]() 是等比数列;
是等比数列;
⑵若数列![]() 是等比数列,求
是等比数列,求![]() ,
,![]() 的值;
的值;
⑶若![]() ,且
,且![]() ,求证:数列
,求证:数列![]() 是等差数列.
是等差数列.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了检验学习情况,某培训机构于近期举办一场竞赛活动,分别从甲、乙两班各抽取10名学员的成绩进行统计分析,其成绩的茎叶图如图所示(单位:分),假设成绩不低于90分者命名为“优秀学员”.
(1)分别求甲、乙两班学员成绩的平均分(结果保留一位小数);
(2)从甲班4名优秀学员中抽取两人,从乙班2名80分以下的学员中抽取一人,求三人平均分不低于90分的概率.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,以
中,以![]() 为极点,
为极点,![]() 轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线![]() 的极坐标方程为
的极坐标方程为![]() ;直线
;直线![]() 的参数方程为
的参数方程为 (
(![]() 为参数),直线
为参数),直线![]() 与曲线
与曲线![]() 分别交于
分别交于![]() ,
,![]() 两点.
两点.
(1)写出曲线![]() 的直角坐标方程和直线
的直角坐标方程和直线![]() 的普通方程;
的普通方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,
,![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com