
【题目】已知数列![]() ,其前
,其前![]() 项和为
项和为![]() ,满足
,满足![]() ,
,![]() ,其中
,其中![]() ,
,![]() ,
,![]() ,
,![]() .
.
⑴若![]() ,
,![]() ,
,![]() (
(![]() ),求证:数列
),求证:数列![]() 是等比数列;
是等比数列;
⑵若数列![]() 是等比数列,求
是等比数列,求![]() ,
,![]() 的值;
的值;
⑶若![]() ,且
,且![]() ,求证:数列
,求证:数列![]() 是等差数列.
是等差数列.
【答案】(1)见解析(2)![]() (3)见解析
(3)见解析
【解析】试题分析:(1)![]() (
(![]() ), 所以
), 所以![]() ,故数列
,故数列![]() 是等比数列;(2)利用特殊值法,得
是等比数列;(2)利用特殊值法,得![]() ,故
,故![]() ;(3)得
;(3)得![]() ,所以
,所以![]() ,得
,得![]() ,可证数列
,可证数列![]() 是等差数列.
是等差数列.
试题解析:
(1)证明:若![]() ,则当
,则当![]() (
(![]() ),
),
所以![]() ,
,
即![]() ,
,
所以![]() ,
,
又由![]() ,
,![]() ,
,
得![]() ,
,![]() ,即
,即![]() ,
,
所以![]() ,
,
故数列![]() 是等比数列.
是等比数列.
(2)若![]() 是等比数列,设其公比为
是等比数列,设其公比为![]() (
(![]() ),
),
当![]() 时,
时,![]() ,即
,即![]() ,得
,得
![]() , ①
, ①
当![]() 时,
时,![]() ,即
,即![]() ,得
,得
![]() , ②
, ②
当![]() 时,
时,![]() ,即
,即![]() ,得
,得
![]() , ③
, ③
②①![]() ,得
,得![]() ,
,
③②![]() ,得
,得![]() ,
,
解得![]() .
.
代入①式,得![]() .
.
此时![]() (
(![]() ),
),
所以![]() ,
,![]() 是公比为1的等比数列,
是公比为1的等比数列,
故![]() .
.
(3)证明:若![]() ,由
,由![]() ,得
,得![]() ,
,
又![]() ,解得
,解得![]() .
.
由![]() ,
,![]() ,
, ![]() ,
,![]() ,代入
,代入![]() 得
得![]() ,
,
所以![]() ,
,![]() ,
,![]() 成等差数列,
成等差数列,
由![]() ,得
,得![]() ,
,
两式相减得:![]()
即![]()
所以![]()
相减得:![]()
所以![]()
所以![]()
![]() ,
,
因为![]() ,所以
,所以![]() ,
,
即数列![]() 是等差数列.
是等差数列.


科目:高中数学 来源: 题型:
【题目】(本小题满分16分)
已知数列{an}的前n项和为Sn,且a1=1,Sn=n2an(n∈N*).
(1)试求出S1,S2,S3,S4,并猜想Sn的表达式;
(2)用数学纳法证明你的猜想,并求出an的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(数学文卷·2017届湖北省黄冈市高三上学期期末考试第16题) “中国剩余定理”又称“孙子定理”.1852年英国来华传教伟烈亚利将《孙子算经》中“物不知数”问题的解法传至欧洲.1874年,英国数学家马西森指出此法符合1801年由高斯得出的关于同余式解法的一般性定理,因而西方称之为“中国剩余定理”. “中国剩余定理”讲的是一个关于整除的问题,现有这样一个整除问题:将2至2017这2016个数中能被3除余1且被5除余1的数按由小到大的顺序排成一列,构成数列![]() ,则此数列的项数为__________.
,则此数列的项数为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在多面体ABCDEF中,ABCD是正方形,BF⊥平面ABCD,DE⊥平面ABCD,BF=DE,点M为棱AE的中点.
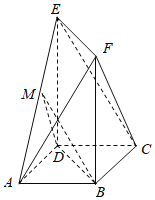
(1)求证:平面BMD∥平面EFC;
(2)若AB=1,BF=2,求三棱锥A-CEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某企业开展技术创新活动,提出了完成某项生产任务的两种新的生产方式.为比较两种生产方式的效率,选取40名技术人员,将他们随机分成两组,每组20人,第一组技术人员用第一种生产方式,第二组技术人员用第二种生产方式.根据他们完成生产任务的工作时间(单位:min)绘制了如下茎叶图:
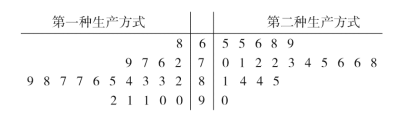
(1)求40名技术人员完成生产任务所需时间的中位数![]() ,并将完成生产任务所需时间超过
,并将完成生产任务所需时间超过![]() 和不超过
和不超过![]() 的人数填入下面的列联表:
的人数填入下面的列联表:
超过 | 不超过 | 合计 | |
第一种生产方式 | |||
第二种生产方式 | |||
合计 |
(2)根据(1)中的列联表,能否有99%的把握认为两种生产方式的效率有差异?
附:![]()
P(K2≥k0) | 0.050 | 0.010 | 0.001 |
k0 | 3.841 | 6.635 | 1.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在某商业区周边有 两条公路![]() 和
和![]() ,在点
,在点![]() 处交汇,该商业区为圆心角
处交汇,该商业区为圆心角![]() ,半径3
,半径3![]() 的扇形,现规划在该商业区外修建一条公路
的扇形,现规划在该商业区外修建一条公路![]() ,与
,与![]() ,
,![]() 分别交于
分别交于![]() ,要求
,要求![]() 与扇形弧相切,切点
与扇形弧相切,切点![]() 不在
不在![]() ,
,![]() 上.
上.
(1)设![]() 试用
试用![]() 表示新建公路
表示新建公路![]() 的长度,求出
的长度,求出![]() 满足的关系式,并写出
满足的关系式,并写出![]() 的范围;
的范围;
(2)设![]() ,试用
,试用![]() 表示新建公路
表示新建公路![]() 的长度,并且确定
的长度,并且确定![]() 的位置,使得新建公路
的位置,使得新建公路![]() 的长度最短.
的长度最短.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数y=f(x)对定义域内的每一个值x1,在其定义域内都存在唯一的x2,使f(x1)f(x2)=1成立,则称该函数为“依赖函数”.
(1) 判断函数g(x)=2x是否为“依赖函数”,并说明理由;
(2) 若函数f(x)=(x–1)2在定义域[m,n](m>1)上为“依赖函数”,求实数m、n乘积mn的取值范围;
(3) 已知函数f(x)=(x–a)2 (a<![]() )在定义域[
)在定义域[![]() ,4]上为“依赖函数”.若存在实数x[
,4]上为“依赖函数”.若存在实数x[![]() ,4],使得对任意的tR,有不等式f(x)≥–t2+(s–t)x+4都成立,求实数s的最大值.
,4],使得对任意的tR,有不等式f(x)≥–t2+(s–t)x+4都成立,求实数s的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列语句是否为命题?如果是,判断它的真假.
(1)这道数学题有趣吗?(2)0不可能不是自然数;(3)![]() ;(4)
;(4)![]() ;
;
(5)91不是素数;(6)上海的空气质量越来越好.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com