定义在R上的函数y=f(x),对于任意实数m,n,恒有f(m+n)=f(m)•f(n),且当x>0时,0<f(x)<1.
(1)求f(0)的值;
(2)求当x<0时,f(x)的取值范围;
(3)判断f(x)在R上的单调性,并证明你的结论.
解:(1)令m=0,n>0,则有f(n)=f(0+n)=f(0)•f(n)
又由已知,n>0时,0<f(n)<1,
∴f (0)=1
(2)设x<0,则-x>0f(0)=f[x+(-x)]=f(x)•f(-x)=1
则

,
又∵-x>0,
∴0<f(-x)<1,
∴f(x)∈(1,+∞)
(3)f(x)在R上的单调递减
证明:设x
1、x
2∈R,且x
1<x
2又x
1=(x
1-x
2)+x
2,由已知f(x
1)=f[(x
1-x
2)+x
2]=f(x
1-x
2)•f(x
2)
∴
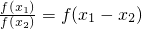
…(16分),
∵x
1<x
2,∴x
1-x
2<0,由(2)得f(x
1-x
2)>1
∴
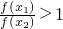
,又由(1)、(2),
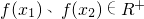
,
∴f(x
1)>f(x
2)
∴f(x)在R上的单调递减
分析:(1)利用赋值法,令m=0,n>0,则有f(n)=f(0+n)=f(0)•f(n)结合题中条件:“n>0时,0<f(n)<1”,即可求出f (0);
(2)根据f(m+n)=f(m)•f(n)恒成立,考虑取x=0代入,可得f(0)=1,再取x=-y,可得f(-y)=
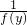
,再结合条件x>0时,有0<f(x)<1,经过变形化简可得x<0时,0<f(x)<1成立.
(3)这是抽象函数的单调性问题,应该用单调性定义解决.对差的符号进行判断时要注意根据其形式结合(2)的结论选择判断的方式.
点评:本小题主要考查函数单调性的应用、抽象函数及其应用、不等式的解法等基础知识,考查运算求解能力,考查化归与转化思想.属于基础题.

 ,
,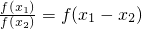 …(16分),
…(16分),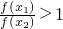 ,又由(1)、(2),
,又由(1)、(2),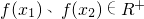 ,
,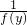 ,再结合条件x>0时,有0<f(x)<1,经过变形化简可得x<0时,0<f(x)<1成立.
,再结合条件x>0时,有0<f(x)<1,经过变形化简可得x<0时,0<f(x)<1成立.

 七星图书口算速算天天练系列答案
七星图书口算速算天天练系列答案