
分析 (1)求出f(x)的导数,由题意可得f′(2)=0,解方程可得a,再由导数大于0,可得增区间;导数小于0,可得减区间;
(2)由f(x)的单调区间,可得f(-1)为极大值b+$\frac{7}{2}$,f(2)为极小值b-10,由b>0且f(x)有两个零点,可得b=10,求得f(x)在x=1处切线的斜率和切点,由点斜式方程即可得到所求切线的方程.
解答 解:(1)函数f(x)=x3+ax2-6x+b(b>0)的导数为
f′(x)=3x2+2ax-6,
由f(x)在x=2处取得极值,
可得f′(2)=12+4a-6=0,
解得a=-$\frac{3}{2}$,
即有f′(x)=3x2-3x-6,
由f′(x)>0,可得x>2或x<-1;
由f′(x)<0,可得-1<x<2.
则f(x)的增区间为(-∞,-1),(2,+∞);减区间为(-1,2);
(2)由f(x)=x3-$\frac{3}{2}$x2-6x+b(b>0),
由f(x)的增区间为(-∞,-1),(2,+∞);减区间为(-1,2),
可得f(-1)为极大值b+$\frac{7}{2}$,f(2)为极小值b-10,
由f(x)有两个零点,可得b-10=0,
即b=10,
f(x)=x3-$\frac{3}{2}$x2-6x+10的导数为f′(x)=3x2-3x-6,
可得f(x)在x=1处的切线斜率为-6,
切点为(1,$\frac{7}{2}$),
则f(x)在x=1处的切线方程为y-$\frac{7}{2}$=-6(x-1),
即为12x+2y-19=0.
点评 本题考查导数的运用:求切线的方程和单调区间、极值,考查方程思想和运算能力,属于中档题.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:高中数学 来源: 题型:填空题
| P(K2≥k0) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 |
| k0 | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{\sqrt{3}}{3}$ | B. | $\frac{\sqrt{3}}{3}$ | C. | $\sqrt{3}$ | D. | -$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {1,3,4,5} | B. | {1,4} | C. | {1,2,4} | D. | {3,5} |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
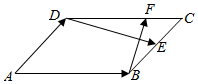 如图,在平行四边形ABCD中,E,F分别是BC,DC上的点,且满足$\overrightarrow{BE}$=$\overrightarrow{EC}$,$\overrightarrow{DF}$=2$\overrightarrow{FC}$,记$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a,\overrightarrow b$为平面向量的一组基底.利用向量的有关知识解决下列问题;
如图,在平行四边形ABCD中,E,F分别是BC,DC上的点,且满足$\overrightarrow{BE}$=$\overrightarrow{EC}$,$\overrightarrow{DF}$=2$\overrightarrow{FC}$,记$\overrightarrow{AB}=\overrightarrow a$,$\overrightarrow{AD}=\overrightarrow b$,试以$\overrightarrow a,\overrightarrow b$为平面向量的一组基底.利用向量的有关知识解决下列问题;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 30 | C. | 40 | D. | 50 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\sqrt{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{\sqrt{5}}{5}$ | D. | $\frac{\sqrt{5}}{25}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com