
【题目】设函数f(x)=a﹣ ![]() ,x∈R,a为常数;
,x∈R,a为常数;
(1)当a=1时,判断f(x)的奇偶性;
(2)求证:f(x)是R上的增函数.
【答案】
(1)解:a=1时,f(x)= ![]() ,
,
f(﹣x)= ![]() =
= ![]() =﹣f(x),
=﹣f(x),
f(x)是奇函数
(2)证明如下:对任意x1,x2∈R,且x1<x2,
则f(x1)﹣f(x2)=(a﹣ ![]() )﹣(a﹣
)﹣(a﹣ ![]() )=
)= ![]() ,
,
∵x1<x2,
∴f(x1)﹣f(x2)<0,
即f(x1)<f(x2),
则函数f(x)为增函数
【解析】(1)当a=1时,根据函数奇偶性的定义即可判断f(x)的奇偶性;(2)根据函数单调性的定义即可证明f(x)是R上的增函数.
【考点精析】掌握函数单调性的判断方法和函数的奇偶性是解答本题的根本,需要知道单调性的判定法:①设x1,x2是所研究区间内任两个自变量,且x1<x2;②判定f(x1)与f(x2)的大小;③作差比较或作商比较;偶函数的图象关于y轴对称;奇函数的图象关于原点对称.


 全能测控期末小状元系列答案
全能测控期末小状元系列答案科目:高中数学 来源: 题型:
【题目】如图,AB是圆O的直径,PB是圆O的切线,过A点作AE∥OP交圆O于E点,PA交圆O于点F,连接PE. 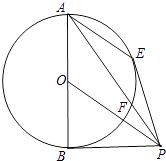
(1)求证:PE是圆O的切线;
(2)设AO=3,PB=4,求PF的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解某社区居民的家庭年收入所年支出的关系,随机调查了该社区5户家庭,得到如表统计数据表:
收入x (万元) | 8.2 | 8.6 | 10.0 | 11.3 | 11.9 |
支出y (万元) | 6.2 | 7.5 | 8.0 | 8.5 | 9.8 |
根据如表可得回归直线方程y= ![]() x+
x+ ![]() ,其中
,其中 ![]() =0.76,
=0.76, ![]() =
= ![]() ﹣
﹣ ![]()
![]() ,据此估计,该社区一户收入为20万元家庭年支出为( )
,据此估计,该社区一户收入为20万元家庭年支出为( )
A.11.4万元
B.11.8万元
C.15.2万元
D.15.6万元
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列四种说法:
①函数y=ax(a>0且a≠1)与函数y=logaax(a>0且a≠1)的定义域相同;
②函数y=x3与y=3x的值域相同;
③函数y= ![]() +
+ ![]() 与y=
与y= ![]() 都是奇函数;
都是奇函数;
④函数y=(x﹣1)2与y=2x﹣1在区间[0,+∞)上都是增函数.
其中正确的序号是(把你认为正确叙述的序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l过点P(0,﹣4),且倾斜角为 ![]() ,圆C的极坐标方程为ρ=4cosθ.
,圆C的极坐标方程为ρ=4cosθ.
(1)求直线l的参数方程和圆C的直角坐标方程;
(2)若直线l和圆C相交于A、B两点,求|PA||PB|及弦长|AB|的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4x+a2x+3,a∈R
(1)当a=﹣4时,且x∈[0,2],求函数f(x)的值域;
(2)若f(x)>0在(0,+∞)对任意的实数x恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4-4:坐标系与参数方程
在平面直角坐标系中,曲线![]() 的普通方程为
的普通方程为![]() ,曲线
,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),以坐标原点
为参数),以坐标原点![]() 为极点,以
为极点,以![]() 轴正半轴为极轴,建立极坐标系.
轴正半轴为极轴,建立极坐标系.
(1)求曲线![]() 、
、![]() 的极坐标方程;
的极坐标方程;
(2)求曲线![]() 与
与![]() 交点的极坐标,其中
交点的极坐标,其中![]() ,
, ![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】关于函数f(x)=lg ![]() (x≠0,x∈R)有下列命题:
(x≠0,x∈R)有下列命题:
①函数y=f(x)的图象关于y轴对称;
②在区间(﹣∞,0)上,函数y=f(x)是减函数;
③函数f(x)的最小值为lg2;
④在区间(1,+∞)上,函数f(x)是增函数.
其中正确命题序号为 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com