
如图,把边长为10的正六边形纸板剪去相同的六个角,做成一个底面为正六边形的无盖六棱柱盒子,设其高为h,体积为V(不计接缝).
(1)求出体积V与高h的函数关系式并指出其定义域;
(2)问当 为多少时,体积V最大?最大值是多少?
为多少时,体积V最大?最大值是多少?

科目:高中数学 来源:2015届山东省威海市高二下学期期末考试理科数学试卷(解析版) 题型:选择题
曲线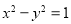 经过伸缩变换T得到曲线
经过伸缩变换T得到曲线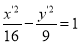 ,那么直线
,那么直线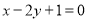 经过伸缩变换T得到的直线方程为( )
经过伸缩变换T得到的直线方程为( )
A.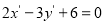 B.
B.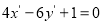
C.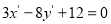 D.
D.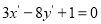
查看答案和解析>>
科目:高中数学 来源:2015届山东省乳山市高二下学期中考试理科数学试卷(解析版) 题型:选择题
定义:若存在常数 ,使得对定义域
,使得对定义域 内的任意两个
内的任意两个 ,均有
,均有 成立,则称函数
成立,则称函数 在定义域
在定义域 上满足利普希茨条件.若函数
上满足利普希茨条件.若函数 满足利普希茨条件,则常数
满足利普希茨条件,则常数 的最小值为( )
的最小值为( )
A.4 B.3 C.1 D.
查看答案和解析>>
科目:高中数学 来源:2015届山东省乳山市高二下学期中考试理科数学试卷(解析版) 题型:选择题
由直线与圆相切时,圆心到切点连线与直线垂直,想到平面与球相切时,球心与切点连线与平面垂直,用的是( )
A.归纳推理 B.演绎推理 C.类比推理 D.传递性推理
查看答案和解析>>
科目:高中数学 来源:2015届山东济宁鱼台二中高二3月质量检测理科数学试卷(解析版) 题型:选择题
已知 为平面内两定点,过该平面内动点
为平面内两定点,过该平面内动点 作直线
作直线 的垂线,垂足为
的垂线,垂足为 .若
.若 ,其中
,其中 为常数,则动点
为常数,则动点 的轨迹不可能是( )
的轨迹不可能是( )
A.圆 B.椭圆 C.抛物线 D.双曲线
查看答案和解析>>
科目:高中数学 来源:2015届山东济宁任城一中高二下学期期中检测理科数学试卷(解析版) 题型:填空题
直线y=a与函数f(x)=x3-3x的图像有相异的三个公共点,则a的取值范围是_____
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com