
分析 (Ⅰ)求出函数的导数,通过讨论k的范围,确定函数的单调区间,从而求出函数的极值即可;
(Ⅱ)不妨设x1<k<x2<k+1,问题转化为证明2k-x1>x2,即证f(2k-x1)>f(x2),根据函数的单调性证明即可.
解答 解:(Ⅰ)∵f'(x)=(x-k)ex,x>0.(1分)
(i)当k≤0时,f'(x)>0恒成立,
∴f(x)的递增区间是(0,+∞),无递减区间;无极值.(3分)
(ii)当k>0时,由f'(x)>0得,x>k;由f'(x)<0得,0<x<k;
∴f(x)的递减区间是(0,k),递増区间是(k,+∞),f(x)的极小值为f(k)=-ek,无极大值.(5分)
(Ⅱ)由已知f(x1)=f(x2)(x1≠x2),
结合(Ⅰ)可知,k>0,f(x)在(-∞,k)上单调递减,在(k,+∞)上单调递增,
又f(k+1)=0,x<k+1时,f(x)<0.…(6分)
不妨设x1<k<x2<k+1,
此时x2>k,2k-x1>k,
故要证x1+x2<2k,只要证2k-x1>x2,
只要证f(2k-x1)>f(x2),
因f(x1)=f(x2),即证f(2k-x1)>f(x1).(8分)
设g(x)=f(2k-x)-f(x)=$\frac{{(-x+k-1){e^{2k}}}}{e^x}\;-(x-k-1){e^x}\;(x<k)$,
$g'(x)=\frac{{(x-k){e^{2k}}}}{e^x}-(x-k){e^x}$=$\frac{{(x-k)({e^{2k}}-{e^{2x}}\;)}}{{{e^x}\;}}$,(9分)
∴当x<k时,g'(x)<0,g(x)在(-∞,k)上单调递减,(10分)
∴x∈(-∞,k)时,g(x)>g(k)=-ek+ek=0,(11分)
故当x<k时,f(2k-x)>f(x),即f(2k-x1)>f(x1)成立,
∴x1+x2<2k.(12分)
点评 本题主要考查函数、导数、不等式等基本知识;考查运算求解能力、推理论证能力;考查化归与转化思想、函数与方程的思想、分类整合思想、数形结合思想.


 同步练习强化拓展系列答案
同步练习强化拓展系列答案科目:高中数学 来源: 题型:选择题
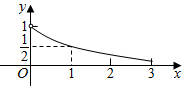 已知奇函数y=$\left\{\begin{array}{l}{{a}^{x},x>0}\\{f(x),x<0}\end{array}\right.$(a>0且a≠1)的部分图象如图所示,那么f(x)=( )
已知奇函数y=$\left\{\begin{array}{l}{{a}^{x},x>0}\\{f(x),x<0}\end{array}\right.$(a>0且a≠1)的部分图象如图所示,那么f(x)=( )| A. | 2x | B. | $-{(\frac{1}{2})^x}$ | C. | ${({\frac{1}{2}})^x}$ | D. | -2x |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
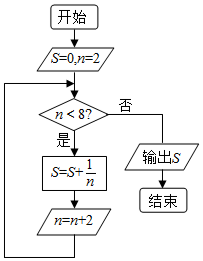 如图所示,执行程序框图,输出结果( )
如图所示,执行程序框图,输出结果( )| A. | $\frac{5}{12}$ | B. | $\frac{7}{12}$ | C. | $\frac{11}{12}$ | D. | 1 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 9 | B. | 12 | C. | 15 | D. | 18 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 平行四边形 | B. | 菱形 | C. | 矩形 | D. | 正方形 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com