
| A. | $\frac{2}{3}$(1-4-n) | B. | $\frac{2}{3}$(1-2-n) | C. | $\frac{2}{3}$(4n-1) | D. | 2n+1-2 |
科目:高中数学 来源: 题型:解答题
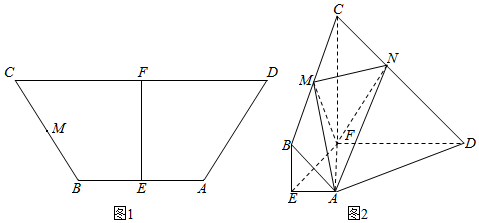
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
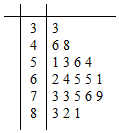 某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,
某公司做了用户对其产品满意度的问卷调查,随机抽取了20名用户的评分,得到如图所示茎叶图,对不低于75的评分,认为用户对产品满意,否则,认为不满意,| 不满意 | 满意 | 合计 | |
| 男 | 4 | 7 | |
| 女 | |||
| 合计 |
| P(K2≥k) | 0.100 | 0.050 | 0.010 |
| k | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
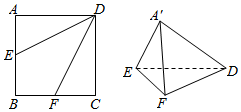 如图,E、F是正方形ABCD的边AB、BC的中点,将△ADE、△CDF、△BEF分别沿DE、DF、EF折起,使A、B、C三点重合于点A′.
如图,E、F是正方形ABCD的边AB、BC的中点,将△ADE、△CDF、△BEF分别沿DE、DF、EF折起,使A、B、C三点重合于点A′.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 如图,一船在海上自西向东航行,在A处测得某岛M的方位角为北偏东α角,前进m千米后在B处测得该岛的方位角为北偏东β角,已知该岛周围n千米范围内(包括边界)有暗礁,现该船继续东行.当α与β满足下列(1)(3)(填序号)条件时,该船没有触礁危险.
如图,一船在海上自西向东航行,在A处测得某岛M的方位角为北偏东α角,前进m千米后在B处测得该岛的方位角为北偏东β角,已知该岛周围n千米范围内(包括边界)有暗礁,现该船继续东行.当α与β满足下列(1)(3)(填序号)条件时,该船没有触礁危险.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| x | 0 | 1 | 2 | 3 | 4 |
| y | 2.2 | 4.3 | t | 4.8 | 6.7 |
| A. | 2.5 | B. | 3.5 | C. | 4.5 | D. | 5.5 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com