
���� �����������֪��c=1��e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$����a=$\sqrt{2}$��b2=a2-c2=1�����������Բ���̣����حAF1ح=$\sqrt{2}$����ֱ��BF2�ķ��̣�������Բ���̣��������B�����꣬�������
حBF2ح���������$\frac{|A{F}_{1}|}{|B{F}_{2}|}$��ֵ��
����������ɵã���ֱ��AP�ķ��̣�������Բ���̣�����ֱ�ߵ�б�ʹ�ʽ��Τ�ﶨ���ɵ�${k}_{A{F}_{1}}$-${k}_{B{F}_{2}}$=0����ֱ��AF1��BF2ƽ�У�
��� �⣺�����������֪��c=1����Բ��������e=$\frac{c}{a}$=$\frac{\sqrt{2}}{2}$����a=$\sqrt{2}$��
b2=a2-c2=1��
����Բ�ı����̣�$\frac{{x}^{2}}{2}+{y}^{2}=1$��
��A��0��1����F1��-1��0����حAF1ح=$\sqrt{2}$��
��ֱ��AF1��б��k=$\frac{1-0}{0-��-1��}$=1����ֱ��BF2�ķ���y=x-1��
$\left\{\begin{array}{l}{y=x-1}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$����ã�$\left\{\begin{array}{l}{x=\frac{4}{3}}\\{y=\frac{1}{3}}\end{array}\right.$��$\left\{\begin{array}{l}{x=0}\\{y=1}\end{array}\right.$��
��A��B��P��λ��x��ͬ�ࣩ��B��$\frac{4}{3}$��$\frac{1}{3}$����
حBF2ح=$\sqrt{��\frac{4}{3}-1��^{2}+��\frac{1}{3}-0��^{2}}$=$\frac{\sqrt{2}}{3}$��
��$\frac{|A{F}_{1}|}{|B{F}_{2}|}$=$\frac{\sqrt{2}}{\frac{\sqrt{2}}{3}}$=3
$\frac{|A{F}_{1}|}{|B{F}_{2}|}$��ֵ3��
������ֱ��AP�����㣨-2��0������ֱ��AP��y=k��x+2������A��x1��y1����P��x2��y2����
��BP��y�ᣬ��B��-x2��y2����
$\left\{\begin{array}{l}{y=k��x+2��}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$���������1+2k2��x2+8k2x+8k2-2=0��
x1+x2=-$\frac{8{k}^{2}}{1+2{k}^{2}}$��x1x2=$\frac{8{k}^{2}-2}{1+2{k}^{2}}$��
��AF1���${k}_{A{F}_{1}}$=$\frac{{y}_{1}-0}{{x}_{1}+1}$��BF2���${k}_{B{F}_{2}}$=$\frac{{y}_{2}}{-{x}_{2}-1}$��
��${k}_{A{F}_{1}}$-${k}_{B{F}_{2}}$=$\frac{{y}_{1}}{{x}_{1}+1}$+$\frac{{y}_{2}}{{x}_{2}+1}$=$\frac{{y}_{1}��{x}_{2}+1��+{y}_{2}��{x}_{1}+1��}{��{x}_{1}+1����{x}_{2}+1��}$��
��y2��x1+1��+��x2+1��y1=k2��x2+2����x1+1��+��x2+1����k1��x1+2��=k[2x1x2+3��x1+x2��+4]
=k[2��$\frac{8{k}^{2}-2}{1+2{k}^{2}}$+3����-$\frac{8{k}^{2}}{1+2{k}^{2}}$��+4]=0��
��${k}_{A{F}_{1}}$=${k}_{B{F}_{2}}$��
��ֱ��AF1��BF2ƽ�У�
���� ���⿼����Բ�ı����̣�ֱ������Բ��λ�ù�ϵ������Τ�ﶨ����ֱ�ߵ�б�ʹ�ʽ��������������������е��⣮


 ���ĺ����Ͼ�������ϵ�д�
���ĺ����Ͼ�������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ֲ���Ҫ���� | B�� | ��Ҫ��������� | ||
| C�� | �Ȳ����Ҳ����Ҫ���� | D�� | ��Ҫ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{{n^2}+5n}}{2}$ | B�� | $\frac{{{n^2}+5n}}{4}$ | C�� | $\frac{{{n^2}+3n}}{2}$ | D�� | $\frac{{{n^2}+3n}}{4}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
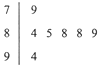 ��ͼ��2015���տ����оٰ��������˶����ϣ�7λ����Ϊij������Ա����ķ����ľ�Ҷͼ��������ֱ�ʾʮλ���֣��ұ����ֱ�ʾ��λ���֣���Щ���ݵ���λ����______��ȥ��һ����ͷֺ���߷ֺ���ʣ���ݵ�ƽ�����ǣ�������
��ͼ��2015���տ����оٰ��������˶����ϣ�7λ����Ϊij������Ա����ķ����ľ�Ҷͼ��������ֱ�ʾʮλ���֣��ұ����ֱ�ʾ��λ���֣���Щ���ݵ���λ����______��ȥ��һ����ͷֺ���߷ֺ���ʣ���ݵ�ƽ�����ǣ�������| A�� | 86.5�� 86.7 | B�� | 88�� 86.7 | C�� | 88��86.8 | D�� | 86.5��86.8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��2$\sqrt{2}$��+�ޣ� | B�� | ��-�ޣ�-2$\sqrt{2}$���ȣ�2$\sqrt{2}$��+�ޣ� | C�� | ��-2$\sqrt{2}$��2���ȣ�2$\sqrt{2}$��+�ޣ� | D�� | ��-�ޣ�-2���ȣ�2��+�ޣ� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��-�ޣ�2�� | B�� | $��-�ޣ�\frac{1}{2}��$ | C�� | $��0��\frac{1}{2}��$ | D�� | $��\frac{1}{2}��+�ޣ�$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{4}{5}$ | B�� | $\frac{4}{5}i$ | C�� | $\frac{6}{5}$ | D�� | $\frac{6}{5}i$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com