
分析 (1)设双曲线C的焦距为2c,运用离心率公式和a,b,c的关系,解方程可得a,b,进而得到双曲线的标准方程;
(2)将直线l的方程代入双曲线的方程,可得x的二次方程,运用韦达定理和判别式大于0,由中点坐标公式可得CD的中点M的坐标,由题意可得直线l与直线AM垂直,运用两直线垂直的条件:斜率之积为-1,可得k,m的关系式,代入判别式大于0的式子,解不等式即可得到所求范围.
解答 解:(1)设双曲线C的焦距为2c,
由题意得2c=4,$\frac{c}{a}=\frac{{2\sqrt{3}}}{3}$,
所以c=2,$a=\sqrt{3}$,b=$\sqrt{{c}^{2}-{a}^{2}}$=1,
所以双曲线C的标准方程为$\frac{x^2}{3}-{y^2}=1$.
(2)联立$\left\{{\begin{array}{l}{y=kx+m}\\{\frac{x^2}{3}-{y^2}=1}\end{array}}\right.$,得(3k2-1)x2+6kmx+3(m2+1)=0,
首先应有$\left\{{\begin{array}{l}{3{k^2}-1≠0}\\{△={{(6km)}^2}-4(3{k^2}-1)×3({m^2}+1)>0}\end{array}}\right.$,
即$\left\{{\begin{array}{l}{3{k^2}-1≠0}\\{{m^2}-3{k^2}+1>0}\end{array}}\right.$(※),
设点C(x1,y1),D(x2,y2),线段CD的线段为M(x0,y0),
由韦达定理得${x_1}+{x_2}=\frac{-6km}{{3{k^2}-1}}$,
所以${x_0}=\frac{-3km}{{3{k^2}-1}}$,${y_0}=k{x_0}+m=\frac{-m}{{3{k^2}-1}}$,
所以点$M(\frac{-3km}{{3{k^2}-1}},\frac{-m}{{3{k^2}-1}})$,
可得直线AM的斜率为${k_{AM}}═\frac{{\frac{-m}{{3{k^2}-1}}+1}}{{\frac{-3km}{{3{k^2}-1}}}}=\frac{{3{k^2}-m-1}}{-3km}$,
由题意应有直线l与直线AM垂直,所以kAM•k=-1,
即$\frac{{3{k^2}-m-1}}{-3km}•k=-1$,
化简得3k2=4m+1,因为3k2>0,
所以4m+1>0,解得$m>-\frac{1}{4}$.
将3k2=4m+1代入(※)式得$\left\{{\begin{array}{l}{4m+1-1≠0}\\{{m^2}-(4m+1)+1>0}\end{array}}\right.$,
解得m<0或m>4.
故m的取值范围是$\left\{{m\left|{-\frac{1}{4}<m<0,或m>4}\right.}\right\}$.
点评 本题考查双曲线的方程的求法,注意运用离心率公式和a,b,c的关系,考查直线方程和双曲线的方程联立,运用韦达定理和中点坐标公式,考查化简整理的运算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
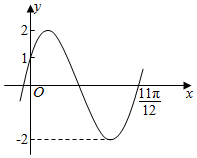
| A. | ω=$\frac{10}{11}$,φ=$\frac{π}{6}$ | B. | ω=$\frac{10}{11}$,φ=-$\frac{π}{6}$ | C. | ω=2,φ=$\frac{π}{6}$ | D. | ω=2,φ=-$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2x+y-2=0 | B. | 2x+y+2=0 | C. | x+2y+2=0 | D. | x+2y-2=0 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (1,2) | C. | (1,1+$\sqrt{2}$) | D. | (2,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{2}$ | B. | $\frac{{\sqrt{6}}}{2}$ | C. | 3 | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{3}$ | B. | $\frac{{3\sqrt{5}}}{5}$ | C. | $\frac{{\sqrt{6}}}{3}$ | D. | $\frac{{\sqrt{6}}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 我校一名学霸在本次考试之前的所有考试中,都考了第一名;所以本次考试他一定能考第一名 | |
| B. | 一枚硬币掷一次得到正面的概率是$\frac{1}{2}$,那么掷两次一定会出现一次正面的情况 | |
| C. | 如买彩票中奖的概率是万分之一,则买一万元的彩票一定会中奖一元 | |
| D. | 随机事件发生的概率与试验次数无关 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com