

科目:高中数学 来源:不详 题型:解答题
 0分)选修4-1:几何证明选讲
0分)选修4-1:几何证明选讲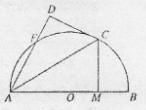
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 上,与x轴的另一个交点为A,△MOA为等腰直角三角形,求圆M的方程.
上,与x轴的另一个交点为A,△MOA为等腰直角三角形,求圆M的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 AD·AE,求∠BAC的大小。
AD·AE,求∠BAC的大小。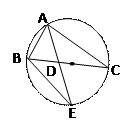
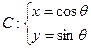
 为参数且(0≤
为参数且(0≤ ≤
≤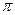 )
)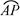 P为半圆C上一点,A(1,0)O为坐标原点,点M在射线OP上,线段OM与 的长度均为
P为半圆C上一点,A(1,0)O为坐标原点,点M在射线OP上,线段OM与 的长度均为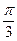 。
。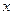 轴为正半轴为极轴建立极坐标系求点M的极坐标。
轴为正半轴为极轴建立极坐标系求点M的极坐标。
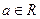
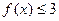 的解集为
的解集为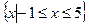 求a值。
求a值。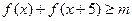 对一切实数
对一切实数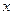 恒成立,求实数m的取值范围。
恒成立,求实数m的取值范围。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com