
| A. | $\frac{5}{2}$ | B. | $\frac{7}{3}$ | C. | $\frac{7}{2}$ | D. | 4 |
分析 连接OA,交BC于P,根据三点共线设$\overrightarrow{OP}$=x$\overrightarrow{OB}+(1-x)\overrightarrow{OC}$,$\overrightarrow{OA}=t\overrightarrow{OP}$=xt$\overrightarrow{OB}$+t(1-x)$\overrightarrow{OC}$,利用平面向量的基本定理列方程组解得t即可得出AP,OP的数量关系,从而得出三角形的面积比.
解答 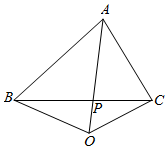 解:连接OA,交BC于P,
解:连接OA,交BC于P,
∵B,P,C三点共线,不妨设$\overrightarrow{OP}$=x$\overrightarrow{OB}+(1-x)\overrightarrow{OC}$,
又A,P,O三点共线,设$\overrightarrow{OA}=t\overrightarrow{OP}$=xt$\overrightarrow{OB}$+t(1-x)$\overrightarrow{OC}$,
∵$\overrightarrow{OA}$=3$\overrightarrow{OB}$+$\frac{3}{2}$$\overrightarrow{OC}$
∴$\left\{\begin{array}{l}{xt=3}\\{t(1-x)=\frac{3}{2}}\end{array}\right.$,解得t=$\frac{9}{2}$.
∴O在AP的延长线上.
∴AP=$\frac{7}{2}$OP.
∴$\frac{{S}_{△ABC}}{{S}_{△OBC}}=\frac{AP}{OP}$=$\frac{7}{2}$.
故选:C.
点评 本题考查了平面向量的基本定理,向量线性运算的几何意义,属于中档题.


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
冲刺100分单元优化练考卷系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
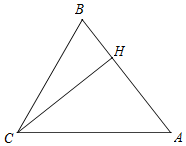 已知三角形△ABC中,∠ACB=60°,CH为AB边上的高,H为垂足;设BC=a,CA=b,AB=c,CH=h;
已知三角形△ABC中,∠ACB=60°,CH为AB边上的高,H为垂足;设BC=a,CA=b,AB=c,CH=h;查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC为等边三角形,AE=1,BD=2,CD与平面ABCDE所成角的正弦值为$\frac{{\sqrt{6}}}{4}$.
如图,在多面体ABCDE中,DB⊥平面ABC,AE∥DB,且△ABC为等边三角形,AE=1,BD=2,CD与平面ABCDE所成角的正弦值为$\frac{{\sqrt{6}}}{4}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com