
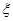 和
和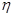 ,其中
,其中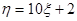 ,且
,且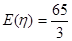 ,若
,若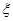 的分布列如右表,则
的分布列如右表,则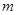 的值为
的值为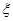 | 1 | 2 | 3 | 4 |
| P | 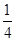 | 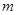 | 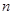 | 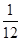 |
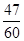 B.
B.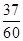 C.
C.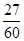 D.
D.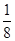
科目:高中数学 来源:不详 题型:解答题
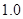 倍、
倍、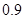 倍、
倍、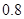 倍的概率分别为
倍的概率分别为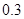 、
、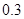 、
、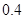 ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的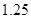 倍、
倍、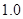 倍的概率分别为
倍的概率分别为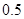 、
、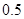 。若实施方案二,预计第一年可以使出口额恢复到危机前的
。若实施方案二,预计第一年可以使出口额恢复到危机前的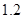 倍、
倍、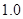 倍、
倍、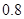 倍的概率分别为
倍的概率分别为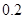 、
、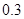 、
、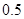 ;第二年可以使出口额为第一年的
;第二年可以使出口额为第一年的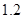 倍、
倍、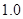 倍的概率分别为
倍的概率分别为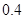 、
、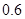 。实施每种方案第一年与第二年相互独立。令
。实施每种方案第一年与第二年相互独立。令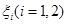 表示方案
表示方案 实施两年后出口额达到危机前的倍数。
实施两年后出口额达到危机前的倍数。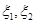 的分布列;
的分布列;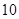 万元、
万元、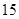 万元、
万元、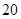 万元,问实施哪种方案的平均利润更大?
万元,问实施哪种方案的平均利润更大?查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 男 | 女 | 总计 |
| 看营养说明 | 50 | 30 | 80 |
| 不看营养说明 | 10 | 20 | 30 |
| 总计 | 60 | 50 | 110 |
 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
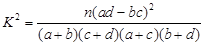 ,其中
,其中 )
)
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
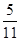 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
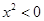 ”是不可能事件
”是不可能事件| A.0 | B.1 | C.2 | D.3 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
| A.5个 | B.15个 | C.10个 | D.8个 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
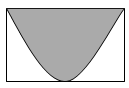
A.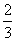 | B.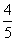 |
C.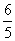 | D.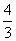 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com