
分析 根据不等式ax2+bx+c≤M(a<0)有唯一实数解,即最大值$\frac{{b}^{2}-4ac}{4a}$=M;不等式ax2+bx+c≤M(a>0)有唯一实数解?最小值$\frac{{b}^{2}-4ac}{4a}$=M,可以判断实数k的取值,要对参数k进行分类讨论,以确定不等式的类型,在各种情况中分别解答后,综合结论即得最终结果.
解答 解:若k=0,不等式组1≤kx2+2x+k≤2可化为:1≤2x≤2,不满足条件.
若k>0,则若不等式组1≤kx2+2x+k≤2,$\frac{4-4{k}^{2}}{4k}$=2时,满足条件.
此时解得:k=$1+\sqrt{2}$
若k<0,则若不等式组1≤kx2+2x+k≤2,$\frac{4-4{k}^{2}}{4k}$=1时,满足条件
此时解得:k=$\frac{1-\sqrt{5}}{2}$
所以:实数k的取值集合{$1+\sqrt{2}$,$\frac{1-\sqrt{5}}{2}$}
故答案为{$1+\sqrt{2}$,$\frac{1-\sqrt{5}}{2}$}.
点评 本题考查了不等式ax2+bx+c≤M(a<0)有唯一实数解,最大值$\frac{{b}^{2}-4ac}{4a}$=M;不等式ax2+bx+c≤M(a>0)有唯一实数解,最小值$\frac{{b}^{2}-4ac}{4a}$=M.属于基础题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{5}}}{5}$ | B. | $\frac{{\sqrt{5}}}{3}$ | C. | $\frac{{2\sqrt{5}}}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
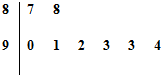 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91、5 | B. | 91、5.5 | C. | 92、5.5 | D. | 92、5 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | $\sqrt{21}$ | C. | $\sqrt{53}$ | D. | $\sqrt{61}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{3}$ | B. | $\frac{4}{3}$ | C. | $\frac{2}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4$\sqrt{3}$ | B. | -4$\sqrt{3}$ | C. | $\frac{4\sqrt{3}}{3}$ | D. | -$\frac{4\sqrt{3}}{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com