
【题目】如图,四棱锥E﹣ABCD中,底面ABCD为正方形,EC⊥平面ABCD,AB= ![]() ,CE=1,G为AC与BD交点,F为EG中点, (Ⅰ)求证:CF⊥平面BDE;
,CE=1,G为AC与BD交点,F为EG中点, (Ⅰ)求证:CF⊥平面BDE;
(Ⅱ)求二面角A﹣BE﹣D的大小.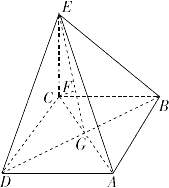
【答案】解:(Ⅰ)证明:∵ABCD为正方形, ![]() , ∴AC=2,AC⊥BD,则CG=1=EC,
, ∴AC=2,AC⊥BD,则CG=1=EC,
∵又F为EG中点,∴CF⊥EG.
∵EG⊥面ABCD,AC∩BD=G,BD⊥平面ECF,
∴CF⊥BDBD∩EG=G,∴CF⊥平面BDE
(Ⅱ)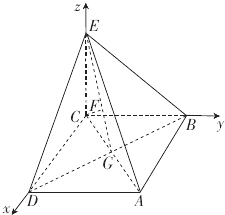
建立如图所示的空间直角坐标系C(0,0,0), 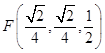 ,
, ![]() [,
[, ![]() ,E(0,0,1)
,E(0,0,1)
由(Ⅰ)知, 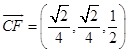 为平面BDE的一个法向量
为平面BDE的一个法向量
设平面ABE的法向量n=(x,y,z),
则 ![]() 即
即 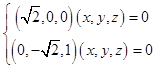
∴ ![]() ∴
∴ ![]()
从而 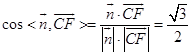 ∴二面角A﹣BE﹣D的大小为
∴二面角A﹣BE﹣D的大小为 ![]() .
.
【解析】(Ⅰ)先用BD垂直于平面ACE证出CF⊥BD,在直角三角形ECG中证明CF⊥EG,即可由线面垂直的判定定理证明CF⊥平面BDE;(Ⅱ)本题作二面角的平面角不易作出,但图形的结构易于建立空间坐标系,故建立如图的空间坐标系,求出两个平面的法向量由数量积公式求解二面角即可
【考点精析】解答此题的关键在于理解直线与平面垂直的判定的相关知识,掌握一条直线与一个平面内的两条相交直线都垂直,则该直线与此平面垂直;注意点:a)定理中的“两条相交直线”这一条件不可忽视;b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】若函数y=f(x)的定义域是[0,2],则函数g(x)= ![]() 的定义域是( )
的定义域是( )
A.[0,1]
B.[0,1)
C.[0,1)∪(1,4]
D.(0,1)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,CD=1,∠BCD=60°,BD⊥CD,正方形ADEF,且面ADEF⊥面ABCD. 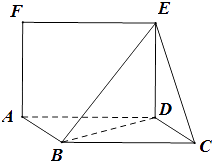
(Ⅰ)求证:BD⊥平面ECD.
(Ⅱ)求D点到面CEB的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,设角A,B,C的对边分别为a,b,c,向量 ![]() =(cosA,sinA),
=(cosA,sinA), ![]() =(
=( ![]() ﹣sinA,cosA),若
﹣sinA,cosA),若 ![]()
![]() =1.
=1.
(1)求角A的大小;
(2)若b=4 ![]() ,且c=
,且c= ![]() a,求△ABC的面积.
a,求△ABC的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有下列说法: ①函数y=﹣cos2x的最小正周期是π;
②终边在y轴上的角的集合是{α|α= ![]() ,k∈Z};
,k∈Z};
③在同一直角坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点;
④函数f(x)=4sin(2x+ ![]() )(x∈R)可以改写为y=4cos(2x﹣
)(x∈R)可以改写为y=4cos(2x﹣ ![]() );
);
⑤函数y=sin(x﹣ ![]() )在[0,π]上是减函数.
)在[0,π]上是减函数.
其中,正确的说法是 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂生产一种机器的固定成本为5000元,且每生产100部,需要加大投入2500元.对销售市场进行调查后得知,市场对此产品的需求量为每年500部,已知销售收入函数为 ![]() ,其中x是产品售出的数量0≤x≤500.
,其中x是产品售出的数量0≤x≤500.
(1)若为x年产量,y表示利润,求y=f(x)的解析式
(2)当年产量为何值时,工厂的年利润最大?其最大值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设全集为R,A={x|2x2﹣9x+4≤0},B={x|x2+a<0}.
(1)当a=﹣9时,求A∩B,(RA)∪B;
(2)当a<0时,若(RA)∩B=B,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知复数Z=(m2+5m+6)+(m2﹣2m﹣15)i,当实数m为何值时:
(1)Z为实数;
(2)Z为纯虚数;
(3)复数Z对应的点Z在第四象限.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com