
分析 (1)根据函数的对称性即可求出g(x),即可得到f(g(x))=x,解得即可.
(2)先求出函数的解析式,得到$\left\{\begin{array}{l}{{m}^{2}=2m}\\{{n}^{2}=2n}\end{array}\right.$,解得m=0,n=2,
(3)由x∈[-1,1]可得t∈[$\frac{1}{2}$,2],结合二次函数的图象和性质,对a进行分类讨论,即可得到函数y=f2(x)-2af(x)+3的最小值h(a)的表达式.
解答 解:(1)∵函数f(x)=($\frac{1}{2}$)x的图象与函数y=g(x)的图象关于直线y=x对称,
∴g(x)=$lo{g}_{\frac{1}{2}}x$,
∵f(g(x))=6-x2,
∴$(\frac{1}{2})^{lo{g}_{\frac{1}{2}}x}$=6-x2=x,
即x2+x-6=0,
解得x=2或x=-3(舍去),
故x=2,
(2)y=g(f(x2))=$lo{g}_{\frac{1}{2}}(\frac{1}{{2}^{{x}^{2}}})$=x2,
∵定义域为[m,n](m≥0),值域为[2m,2n],
$\left\{\begin{array}{l}{{m}^{2}=2m}\\{{n}^{2}=2n}\end{array}\right.$,
解得m=0,n=2,
(3)令t=($\frac{1}{2}$)x,
∵x∈[-1,1],
∴t∈[$\frac{1}{2}$,2],
则y=[f(x)]2-2af(x)+3等价为y=m(t)=t2-2at+3,
对称轴为t=a,
当a<$\frac{1}{2}$时,函数的最小值为h(a)=m($\frac{1}{2}$)=$\frac{13}{4}$-a;
当$\frac{1}{2}$≤a≤2时,函数的最小值为h(a)=m(a)=3-a2;
当a>2时,函数的最小值为h(a)=m(2)=7-4a;
故h(a)=$\left\{\begin{array}{l}{7-4a,a>2}\\{-{a}^{2}+3,\frac{1}{2}≤a≤2}\\{-a+\frac{13}{4},a<\frac{1}{2}}\end{array}\right.$
点评 本题考查的知识点是指数函数的图象和性质,二次函数的图象和性质,分段函数,是函数图象和性质的综合应用,难度中档.


科目:高中数学 来源: 题型:解答题
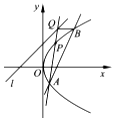 已知直线l的方程为y=x+2,点P是抛物线y2=4x上到直线l距离最小的点,点A是抛物线上异于点P的点,直线AP与直线l交于点Q,过点Q与x轴平行的直线与抛物线y2=4x交于点B.
已知直线l的方程为y=x+2,点P是抛物线y2=4x上到直线l距离最小的点,点A是抛物线上异于点P的点,直线AP与直线l交于点Q,过点Q与x轴平行的直线与抛物线y2=4x交于点B.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
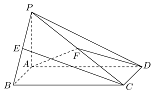 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 恒为偶数 | B. | 恒为奇数 | C. | 不超过2017 | D. | 可超过2017 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-∞,-7]∪[1,+∞) | B. | [-7,1] | C. | (-∞,-1]∪[7,+∞) | D. | [-1,7] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com