
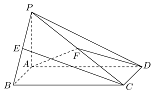
 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与分析 (1)分别以AB、AD、AP所在直线为x、y、z轴建立空间直角坐标系.利用向量$\overrightarrow{EC}$与$\overrightarrow{PD}$所成角求得异面直线EC与PD所成角的大小;
(2)直接利用VP-AFD=VP-ACD-VF-ADC求解.
解答 解:(1) 分别以AB、AD、AP所在直线为x、y、z轴建立空间直角坐标系.
分别以AB、AD、AP所在直线为x、y、z轴建立空间直角坐标系.
∵AP=2,$∠PBA=\frac{π}{4}$,∠PDA=$arctan\frac{1}{2}$,
∴AB=2,AD=4,则P(0,0,2),D(0,4,0),E(1,0,1),C(2,4,0),
$\overrightarrow{EC}=(1,4,-1)$,$\overrightarrow{PD}=(0,4,-2)$.
∴cos<$\overrightarrow{EC},\overrightarrow{PD}$>=$\frac{\overrightarrow{EC}•\overrightarrow{PD}}{|\overrightarrow{EC}||\overrightarrow{PD}|}$=$\frac{18}{\sqrt{18}×2\sqrt{5}}$=$\frac{3\sqrt{10}}{10}$.
∴异面直线EC与PD所成角的大小为$arccos\frac{{3\sqrt{10}}}{10}$;
(2)VP-AFD=VP-ACD-VF-ACD=$\frac{1}{3}×\frac{1}{2}×4×2×2-\frac{1}{3}×\frac{1}{2}×4×2×1$=$\frac{4}{3}$.
点评 本题考查异面直线所成角的求法,训练了利用空间向量求异面直线所成角,是中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 18 | C. | 16 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
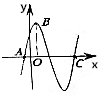 如图,由于函数f(x)=sin(π-ωx)sin($\frac{π}{2}$+φ)-sin(ωx+$\frac{3π}{2}$)sinφ(ω>0)的图象部分数据已污损,现可以确认点C($\frac{5π}{2}$,0),其中A点是图象在y轴左侧第一个与x轴的交点,B点是图象在y轴右侧第一个最高点,则f(x)在下列区间中是单调的( )
如图,由于函数f(x)=sin(π-ωx)sin($\frac{π}{2}$+φ)-sin(ωx+$\frac{3π}{2}$)sinφ(ω>0)的图象部分数据已污损,现可以确认点C($\frac{5π}{2}$,0),其中A点是图象在y轴左侧第一个与x轴的交点,B点是图象在y轴右侧第一个最高点,则f(x)在下列区间中是单调的( )| A. | (0,$\frac{5π}{8}$) | B. | ($\frac{5π}{8}$,$\frac{5π}{3}$) | C. | ($\frac{5π}{3}$,2π) | D. | ($\frac{5π}{3}$,$\frac{5π}{2}$) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com