
分析 (2+x)n(其中n=2,3,4,…)的展开式,Tr+1,令r=2,可得an,再利用求和公式化简,利用数列的极限即可得出.
解答 解:(2+x)n(其中n=2,3,4,…)的展开式,Tr+1=${C}_{n}^{r}{2}^{n-r}{x}^{r}$,令r=2,可得:T3=2n-2${C}_{n}^{2}$x2.
∴an是二项式(2+x)n(其中n=2,3,4,…)的展开式中x的二项式系数,
∴an=${C}_{n}^{2}$=$\frac{n(n-1)}{2}$.
则$\lim_{n→∞}(\frac{1}{a_2}+\frac{1}{a_3}+…+\frac{1}{a_n})$=$\underset{lim}{n→∞}$2$(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+…+\frac{1}{n-1}-\frac{1}{n})$=$\underset{lim}{n→∞}$$(2-\frac{2}{n})$=2.
故答案为:2.
点评 本题考查二项式定理的应用,数列求和,数列的极限的求法,考查计算能力.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}-\frac{1}{2π}$ | B. | $\frac{1}{4}-\frac{1}{2π}$ | C. | $\frac{3}{4}+\frac{1}{2π}$ | D. | $\frac{1}{4}+\frac{1}{2π}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
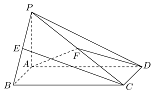 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PB、PD与查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [f(1),f(3)] | B. | [f(1),f($\frac{3}{2}$)] | C. | [c-$\frac{9}{4}$,f(3)] | D. | [f($\frac{3}{2}$),f(3)] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com