
分析 根据题意和公式${a}_{n}=\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$,化简后求出数列的通项公式
解答 解:当n=1时,a1=S1=2-1=1,
当n≥2时,an=Sn-Sn-1=2n-1-(2n-1-1)=2n-1,
又21-1=1,所以an=2n-1,
故答案为:an=2n-1.
点评 本题考查了an、Sn的关系式:${a}_{n}=\left\{\begin{array}{l}{{S}_{1},n=1}\\{{S}_{n}-{S}_{n-1},n≥2}\end{array}\right.$的应用,注意验证n=1是否成立.


 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
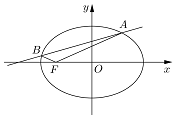 已知椭圆C以原点为中心,左焦点F的坐标是(-1,0),长轴长是短轴长的$\sqrt{2}$倍,直线l与椭圆C交于点A与B,且A、B都在x轴上方,满足∠OFA+∠OFB=180°;
已知椭圆C以原点为中心,左焦点F的坐标是(-1,0),长轴长是短轴长的$\sqrt{2}$倍,直线l与椭圆C交于点A与B,且A、B都在x轴上方,满足∠OFA+∠OFB=180°;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 8 | C. | 16 | D. | 32 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com