
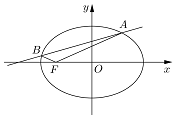
 已知椭圆C以原点为中心,左焦点F的坐标是(-1,0),长轴长是短轴长的$\sqrt{2}$倍,直线l与椭圆C交于点A与B,且A、B都在x轴上方,满足∠OFA+∠OFB=180°;
已知椭圆C以原点为中心,左焦点F的坐标是(-1,0),长轴长是短轴长的$\sqrt{2}$倍,直线l与椭圆C交于点A与B,且A、B都在x轴上方,满足∠OFA+∠OFB=180°;分析 (1)由题意可知设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),2a=$\sqrt{2}$•2b,即a=$\sqrt{2}$b,代入求得:a2=2,b2=1,即可求得椭圆C的标准方程;
(2)B关于x轴的对称点B1在直线AF上.设直线AF方程:y=k(x+1),代入椭圆方程,由韦达定理及直线的斜率公式,代入由x=$\frac{{x}_{2}{y}_{1}-{x}_{1}{y}_{2}}{{y}_{1}-{y}_{2}}$=$\frac{{x}_{2}×k({x}_{1}+1)+{x}_{1}×k({x}_{2}+1)}{k({x}_{1}+1)+k({x}_{2}+1)}$,此能证明直线l总经过定点M(-2,0).
解答 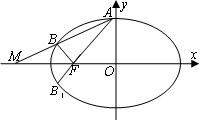 解:(1)设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
解:(1)设椭圆的标准方程为:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0),
由题意可知:2a=$\sqrt{2}$•2b,即a=$\sqrt{2}$b,
由c=1,则a2=b2+c2=b2+1,
代入求得:a2=2,b2=1,
椭圆C的方程为:$\frac{x^2}{2}+{y^2}=1$;
(2)存在一个定点M(-2,0),无论∠OFA如何变化,直线l总经过此定点
证明:由OFA+∠OFB=180°,则B关于x轴的对称点B1在直线AF上.
设A(x1,y1),B(x2,y2),B1(x2,-y2),
设直线AF方程:y=k(x+1),代入$\left\{\begin{array}{l}{y=k(x+1)}\\{\frac{{x}^{2}}{2}+{y}^{2}=1}\end{array}\right.$,
得:(k2+$\frac{1}{2}$)x2+2k2x+k2-1=0,…(13分)
由韦达定理可知:x1+x2=$\frac{2{k}^{2}}{{k}^{2}+\frac{1}{2}}$,x1•x2=$\frac{{k}^{2}-1}{{k}^{2}+\frac{1}{2}}$,
由直线AB的斜率kAB=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$
AB的方程:y-y1=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$(x-x1),
令y=0,得:x=x1-y1•$\frac{{x}_{1}-{x}_{2}}{{y}_{1}-{y}_{2}}$,
y1=k(x1+1),-y2=k(x2+1),
x=$\frac{{x}_{2}{y}_{1}-{x}_{1}{y}_{2}}{{y}_{1}-{y}_{2}}$=$\frac{{x}_{2}×k({x}_{1}+1)+{x}_{1}×k({x}_{2}+1)}{k({x}_{1}+1)+k({x}_{2}+1)}$=$\frac{2{x}_{1}{x}_{2}+{x}_{1}+{x}_{2}}{{x}_{1}+{x}_{2}+2}$=$\frac{2×\frac{{k}^{2}-1}{{k}^{2}+\frac{1}{2}}-\frac{2{k}^{2}}{{k}^{2}+\frac{1}{2}}}{2-\frac{2{k}^{2}}{{k}^{2}+\frac{1}{2}}}$=-2,
∴直线l总经过定点M(-2,0).
点评 本题考查椭圆方程的求法,考查直线方程的求法,考查直线总过定点的证明,解题时要认真审题,注意函数与方程思想的合理运用,考查计算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2a | B. | 3a | C. | $({1+\sqrt{5}})a$ | D. | 4a |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com