
分析 先求出y2的范围,再令y2=t,t≥$\frac{1}{2}$,则f(t)=2+t-$\frac{1}{t}$,根据函数的单调性即可求出范围.
解答 解:${x^2}+\frac{1}{y^2}=2$,则x2+y2=2-$\frac{1}{{y}^{2}}$+y2,
∵${x^2}+\frac{1}{y^2}=2$
∴y2≥$\frac{1}{2}$
设y2=t,t≥$\frac{1}{2}$,
则f(t)=2+t-$\frac{1}{t}$,
∴f′(t)=1+$\frac{1}{{t}^{2}}$>0,
∴f(t)在[$\frac{1}{2}$,+∞)为增函数,
∴f(t)≥f($\frac{1}{2}$)=2+$\frac{1}{2}$-2=$\frac{1}{2}$,
故则x2+y2的取值范围是为[$\frac{1}{2}$,+∞),
故答案为:[$\frac{1}{2}$,+∞)
点评 本题考查了导数和函数的单调性的关系,属于中档题.


 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $[\frac{ln3}{3},\frac{1}{e})$ | B. | $[\frac{ln3}{3},\frac{1}{2e})$ | C. | $(0,\frac{1}{e})$ | D. | $(0,\frac{1}{2e})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
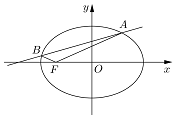 已知椭圆C以原点为中心,左焦点F的坐标是(-1,0),长轴长是短轴长的$\sqrt{2}$倍,直线l与椭圆C交于点A与B,且A、B都在x轴上方,满足∠OFA+∠OFB=180°;
已知椭圆C以原点为中心,左焦点F的坐标是(-1,0),长轴长是短轴长的$\sqrt{2}$倍,直线l与椭圆C交于点A与B,且A、B都在x轴上方,满足∠OFA+∠OFB=180°;查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
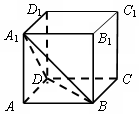 如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在截面A1DB上,则线段AP的最小值等于( )
如图,在棱长为1的正方体ABCD-A1B1C1D1中,点P在截面A1DB上,则线段AP的最小值等于( )| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{2}}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | x+y=0 | B. | x-y+2=0 | C. | x+y-5=0 | D. | x-y=0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com