练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    3．某班级要从4名男生，2名女生中选派4人参加某次社区服务，如果要求至少有1名女生，那么不同的选派方案种数为（　　）
    A．20B．18C．16D．14

    分析 法一：用直接法，4人中至少有1名女生包括1女3男及2女2男两种情况，计算各种情况下的选派方案种数，由加法原理，计算可得答案；
    法二：用排除法，首先计算从4男2女中选4人的选派方案种数，再计算4名都是男生的选派方案种数，由排除法，计算可得答案．

    解答 解：法一：4人中至少有1名女生包括1女3男及2女2男两种情况，
    故不同的选派方案种数为C12•C34+C22•C24=2×4+1×6=14；
    法二：从4男2女中选4人共有C46种选法，4名都是男生的选法有C44种，
    故至少有1名女生的选派方案种数为C46-C44=15-1=14．
    故选D．

    点评 本题考查简单的排列组合，如果分类讨论太复杂的题目最好用间接法即排除法，以避免直接的分类不全情况出现．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    13．在直角坐标系xOy中，设集合Ω={（x，y）|0≤x≤2，0≤y≤1}，在区域Ω内任取一点P（x，y），则满足x+y≥1的概率是$\frac{3}{4}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

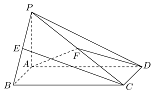    14．如图，在四棱锥P-ABCD中，底面ABCD是矩形，PA⊥平面ABCD，PB、PD与
    平面ABCD所成的角依次是$\frac{π}{4}$和$arctan\frac{1}{2}$，AP=2，E、F依次是PB、PC的中点；
    （1）求异面直线EC与PD所成角的大小；（结果用反三角函数值表示）
    （2）求三棱锥P-AFD的体积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    11．曲线C1：y=sinx，曲线${C_2}：{x^2}+{（y+r-\frac{1}{2}）^2}={r^2}$（r＞0），它们交点的个数（　　）
    A．恒为偶数B．恒为奇数C．不超过2017D．可超过2017

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．已知集合M={（x，y）|y=f（x）}，若对于任意实数对（x1，y1）∈M，存在（x2，y2）∈M，使x1x2+y1y2=0成立，则称集合M是“垂直对点集”．给出下列四个集合：
    ①M={（x，y）|y=$\frac{1}{{x}^{2}}$}； 
    ②M={（x，y）|y=log2x}； 
    ③M={（x，y）|y=2x-2}；
    ④M={（x，y）|y=sinx+1}．
    其中是“垂直对点集”的序号是（　　）
    A．①②③B．①②④C．①③④D．②③④

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．集合{x|1＜x＜6，x∈N*}的非空真子集的个数为14 

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    15．下列判断中正确的是（　　）
    A．$f（x）={（\sqrt{x}）^2}$是偶函数B．$f（x）=\frac{{{x^2}-x}}{x-1}$是奇函数
    C．$f（x）=\frac{{{2^x}+1}}{{{2^x}-1}}$是偶函数D．$f（x）=\frac{{\sqrt{4-{x^2}}}}{|x-3|-3}$是奇函数

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    1．设函数f（x）=|x-3|+|x-a|，如果对任意x∈R，f（x）≥4，则a的取值范围是（　　）
    A．（-∞，-7]∪[1，+∞）B．[-7，1]C．（-∞，-1]∪[7，+∞）D．[-1，7]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    2．已知点P（-2，3），点Q（-6，-1），则直线PQ的倾斜角为（　　）
    A．30°B．45°C．60°D．135°

    查看答案和解析>>

    同步练习册答案