
| A. | $f(x)={(\sqrt{x})^2}$是偶函数 | B. | $f(x)=\frac{{{x^2}-x}}{x-1}$是奇函数 | ||
| C. | $f(x)=\frac{{{2^x}+1}}{{{2^x}-1}}$是偶函数 | D. | $f(x)=\frac{{\sqrt{4-{x^2}}}}{|x-3|-3}$是奇函数 |
分析 根据题意,依次分析选项,对于每一个选项,先求出函数的定义域,再分析f(-x)与f(x)的关系,可得函数的奇偶性,综合即可得答案.
解答 解:根据题意,依次分析选项:
对于A、$f(x)={(\sqrt{x})^2}$,其定义域为{x|x≥0},不关于原点对称,不具有奇偶性,故A错误;
对于B、f(x)=$\frac{{x}^{2}-x}{x-1}$,其定义域为{x|x≠1},不关于原点对称,不具有奇偶性,故B错误;
对于C、f(x)=$\frac{{2}^{x}+1}{{2}^{x}-1}$,其定义域为{x|x≠0},关于原点对称,
f(-x)=$\frac{{2}^{-x}+1}{{2}^{-x}-1}$=$\frac{1+{2}^{x}}{1-{2}^{x}}$=-f(x),f(x)为奇函数,
故C错误;
对于D、函数$f(x)=\frac{{\sqrt{4-{x^2}}}}{|x-3|-3}$,其定义域为{x|-2≤x≤2},关于原点对称,
则f(x)=-$\frac{\sqrt{4-{x}^{2}}}{x}$,f(-x)=-$\frac{\sqrt{4-{x}^{2}}}{x}$=-f(x),
f(x)为奇函数,
故D正确;
故选:D.
点评 本题考查函数奇偶性的判定,注意在判断奇偶性之前要先分析函数的定义域.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | 20 | B. | 18 | C. | 16 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{3}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
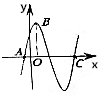 如图,由于函数f(x)=sin(π-ωx)sin($\frac{π}{2}$+φ)-sin(ωx+$\frac{3π}{2}$)sinφ(ω>0)的图象部分数据已污损,现可以确认点C($\frac{5π}{2}$,0),其中A点是图象在y轴左侧第一个与x轴的交点,B点是图象在y轴右侧第一个最高点,则f(x)在下列区间中是单调的( )
如图,由于函数f(x)=sin(π-ωx)sin($\frac{π}{2}$+φ)-sin(ωx+$\frac{3π}{2}$)sinφ(ω>0)的图象部分数据已污损,现可以确认点C($\frac{5π}{2}$,0),其中A点是图象在y轴左侧第一个与x轴的交点,B点是图象在y轴右侧第一个最高点,则f(x)在下列区间中是单调的( )| A. | (0,$\frac{5π}{8}$) | B. | ($\frac{5π}{8}$,$\frac{5π}{3}$) | C. | ($\frac{5π}{3}$,2π) | D. | ($\frac{5π}{3}$,$\frac{5π}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2n-1 | B. | 2n | C. | 2n+1 | D. | n2-n+1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com