
分析 (1)先求出A={1,2},由A∩B={2},得4+4(a+1)+a2-5=0,由此能求出实数a的值.
(2)由A∩B=B,得B=∅,或B={1},或B={2},或B={1,2},分别讨论,能求出实数a的取值范围.
解答 解:(1)A={x||x-$\frac{3}{2}$|=$\frac{1}{2}$}={1,2},
B={t|t2+2(a+1)t+a2-5=0},
∵A∩B={2},∴2是方程t2+2(a+1)t+a2-5=0的根
所以4+4(a+1)+a2-5=0,
解得a=-1或a=-3
当a=-1时B={t|t2-4=0}={-2,2},符合
当a=-3时B={t|t2-4t+4=0}={2},符合
∴实数a的值为-1或-3.
(2)∵A∩B=B,∴B=∅,或B={1},或B={2},或B={1,2},
①当B=∅时,
△=4(a+1)2-4(a2-5)<0,解得a<-3;
②当B={1}时,$\left\{\begin{array}{l}{△=4(a+1)^{2}-4({a}^{2}-5)=0}\\{1+2(a+1)+{a}^{2}-5=0}\end{array}\right.$,无解;
③当B={2}时,$\left\{\begin{array}{l}{△=4(a+1)^{2}-4({a}^{2}-5)=0}\\{4+4(a+1)+{a}^{2}-5=0}\end{array}\right.$,解得a=-3.
③当B={1,2}时,$\left\{\begin{array}{l}{△=4(a+1)^{2}-4({a}^{2}-5)>0}\\{1+2=-2(a+1)}\\{1×2={a}^{2}-5}\end{array}\right.$,无解.
综上,实数a的取值范围是(-∞,-3].
点评 本题考查实数值的求法,是基础题,解题时要认真审题,注意交集的性质和分类讨论思想的合理运用.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
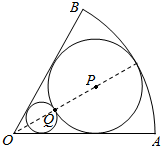 如图,在半径为常数r,圆心角为2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两条半径相切并与圆P外切的小圆Q.
如图,在半径为常数r,圆心角为2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两条半径相切并与圆P外切的小圆Q.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com