
分析 分别求得f1(x),f2(x),f3(x),归纳出fn(fn-1(x)),由代入法可得f2($\frac{1}{2}$);再由分子分母同除以${x}^{{2}^{n}}$,可得fn(x)在[$\frac{1}{2}$,1]上递增,计算即可得到所求最大值.
解答 解:f1(x)=f(x)=$\frac{{x}^{2}}{2x+1}$;
f2(x)=f(f1(x))=$\frac{{x}^{4}}{2{x}^{2}+2x+1}$;
f3(x)=f(f2(x))=$\frac{{x}^{8}}{2{x}^{4}+2{x}^{2}+2x+1}$;
…
fn(fn-1(x))=$\frac{{x}^{{2}^{n}}}{2{x}^{{2}^{n-1}}+2{x}^{{2}^{n-2}}+…+2x+1}$,
则f2($\frac{1}{2}$)=$\frac{\frac{1}{16}}{2×\frac{1}{4}+1+1}$=$\frac{1}{40}$;
fn(x)=$\frac{{x}^{{2}^{n}}}{2{x}^{{2}^{n-1}}+2{x}^{{2}^{n-2}}+…+2x+1}$=$\frac{1}{\frac{2}{x}+\frac{2}{{x}^{2}}+…+\frac{2}{{x}^{{2}^{n-1}}}+\frac{1}{{x}^{{2}^{n}}}}$,
由$\frac{2}{x}$,$\frac{2}{{x}^{2}}$,…,$\frac{2}{{x}^{{2}^{n}-1}}$,$\frac{1}{{x}^{{2}^{n}}}$在[$\frac{1}{2}$,1]递减,可得fn(x)在[$\frac{1}{2}$,1]递增,
即有x=1时,取得最大值,且为$\frac{1}{2+2+…+2+1}$=$\frac{1}{1+2n}$.
故答案为:$\frac{1}{40}$,$\frac{{x}^{4}}{2{x}^{2}+2x+1}$,$\frac{1}{1+2n}$.
点评 本题考查函数值和函数的解析式的求法,注意运用代入法,考查函数的最值的求法,注意运用归纳法和函数的单调性,考查运算能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
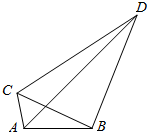 如图,△ABC与△CBD都是直角三角形,∠BAC=∠DBC=90°,∠ABC=∠BDC=30°,若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,求x,y的值.
如图,△ABC与△CBD都是直角三角形,∠BAC=∠DBC=90°,∠ABC=∠BDC=30°,若$\overrightarrow{AD}$=x$\overrightarrow{AB}$+y$\overrightarrow{AC}$,求x,y的值.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com