
分析 由$\overrightarrow{a}$与$\overrightarrow{b}$共线便可得到,存在实数λ,使$\overrightarrow{b}=λ\overrightarrow{a}$,然后根据$|\overrightarrow{a}|=3,|\overrightarrow{b}|=8$即可求出λ,从而可用$\overrightarrow{a}$表示出向量$\overrightarrow{b}$.
解答 解:$\overrightarrow{a}$与$\overrightarrow{b}$共线;
∴$\overrightarrow{b}=λ\overrightarrow{a}$;
∴$|\overrightarrow{b}|=|λ||\overrightarrow{a}|$;
∴$|λ|=\frac{|\overrightarrow{b}|}{|\overrightarrow{a}|}=\frac{8}{3}$;
∴$λ=±\frac{8}{3}$;
∴$\overrightarrow{b}=±\frac{8}{3}\overrightarrow{a}$.
故答案为:$±\frac{8}{3}\overrightarrow{a}$.
点评 考查共线向量基本定理,以及向量的数乘运算.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| A型车 | B型车 | 限量 | |
| 车辆数 | x | y | 0≤x≤8,0≤y≤4 |
| 每天运物吨数 | 24x | 30y | 24x+30y≥180 |
| 每天往返成本费 | 320x | 504y | z |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
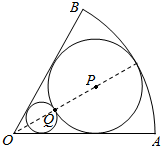 如图,在半径为常数r,圆心角为2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两条半径相切并与圆P外切的小圆Q.
如图,在半径为常数r,圆心角为2θ(0<2θ<π)的扇形OAB内作一内切圆P,再在扇形内作一个与扇形两条半径相切并与圆P外切的小圆Q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com