
在棱长为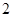 的正方体
的正方体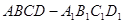 中,
中,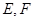 分别为
分别为 的中点.
的中点.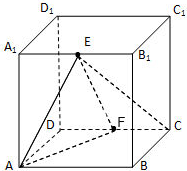
(1)求直线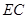 与平面
与平面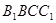 所 成 角的大小;
所 成 角的大小;
(2)求二面角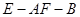 的大小.
的大小.
(1) 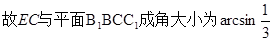 (2)
(2) 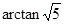
解析试题分析:(1)解法一:建立坐标系
平面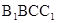 的一个法向量为
的一个法向量为
因为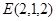
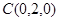 ,
, ,
,
可知直线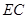 的一个方向向量为
的一个方向向量为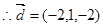 .
.
设直线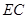 与平面
与平面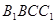 成角为
成角为 ,
, 与
与 所成角为
所成角为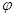 ,则
,则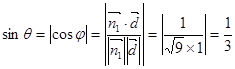
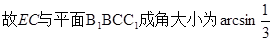
解法二: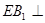 平面
平面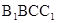 ,即
,即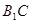 为
为 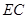 在平面
在平面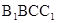 内的射影,
内的射影,
故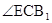 为直线
为直线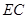 与平面
与平面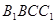 所成角,
所成角,
在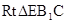 中,
中,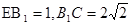 ,
,

(2)解法一:建立坐标系如图.平面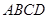 的一个法向量为
的一个法向量为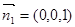
设平面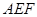 的一个法向量为
的一个法向量为 ,因为
,因为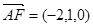 ,
,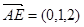
所以 ,令
,令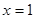 ,则
,则
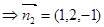
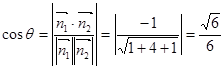
由图知二面角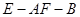 为锐二面角,故其大小为
为锐二面角,故其大小为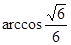 .
.
解法二:过 作平面
作平面 的垂线,垂足为
的垂线,垂足为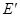 ,
,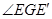 即为所求
即为所求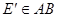 ,过
,过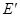 作
作 的垂线设垂足为
的垂线设垂足为 ,
,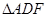 ∽
∽
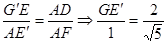 即
即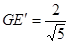 在
在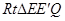 中
中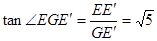
所以 二面角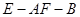 的大小为
的大小为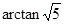 .
.
考点:空间中角的求解
点评:解决的关键是利用角的定义作图来结合几何中的性质定理和判定定理来得到,解三角形得到,或者建立空间直角坐标系,运用向量法来求解。属于中档题。


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:解答题
如图,在长方体ABCD—A1B1C1D1中,AD=AA1=1,AB=2,E为AB的中点,F为CC1的中点.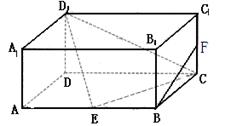
(1)证明:B F//平面E CD1
(2)求二面角D1—EC—D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,△ABC中,AC=BC=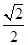 AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.
AB,ABED是边长为1的正方形,EB⊥底面ABC,若G,F分别是EC,BD的中点.
(1)求证:GF∥底面ABC;
(2)求证:AC⊥平面EBC;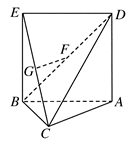
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图所示,已知在矩形ABCD中,AB=1,BC=a(a>0),PA⊥平面AC,且PA=1.

(1)试建立适当的坐标系,并写出点P、B、D的坐标;
(2)问当实数a在什么范围时,BC边上能存在点Q,使得PQ⊥QD?
(3)当BC边上有且仅有一个点Q使得PQ⊥QD时,求二面角Q-PD-A的大小.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在直角梯形ABCD中,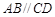 ,
,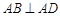 ,且
,且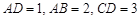 ,E、F分别为线段CD、AB上的点,且
,E、F分别为线段CD、AB上的点,且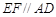 .将梯形沿EF折起,使得平面
.将梯形沿EF折起,使得平面 平面BCEF,折后BD与平面ADEF所成角正切值为
平面BCEF,折后BD与平面ADEF所成角正切值为 .
.
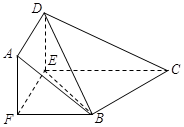
(Ⅰ)求证: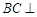 平面BDE;
平面BDE;
(Ⅱ)求平面BCEF与平面ABD所成二面角(锐角)的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com