
分析 (Ⅰ)当a=1时,利用绝对值的意义求得不等式f(x)<3的解集.
(Ⅱ)由条件利用绝对值的意义可得f(x)的最小值为|a+1|=1,由此求得a的值.
解答 解:(Ⅰ)当a=1时,f(x)=|x-1|+|x+1|表示数轴上的x对应点到1、-1对应点的距离之和,
而-$\frac{3}{2}$和$\frac{3}{2}$对应点到1、-1对应点的距离之和正好等于3,故不等式f(x)<3的解集为{x|-$\frac{3}{2}$<x<$\frac{3}{2}$}.
(Ⅱ)函数f(x)=|x-a|+|x+1|表示数轴上的x对应点到a、-1对应点的距离之和,它的最小值为|a+1|=1,
可得a=0,或a=-2.
点评 本题主要考查绝对值的意义,绝对值不等式的解法,属于基础题.


科目:高中数学 来源: 题型:解答题
 为了了解高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率直方图如图所示,已知次数在[100,110)间的频数为7,次数在110以下(不含110)视为不达标,次数在[110,130)视为达标,次数在130以上视为有优秀.
为了了解高一学生的体能情况,某校随机抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出了频率直方图如图所示,已知次数在[100,110)间的频数为7,次数在110以下(不含110)视为不达标,次数在[110,130)视为达标,次数在130以上视为有优秀.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
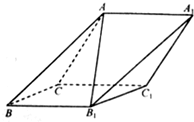 如图,在斜三棱柱 A BC-A1 B1C1中,侧面 ACC1 A1与侧面C B B1C1都是菱形,∠ACC1=∠CC1 B1=60°,AC=2,AB1=$\sqrt{6}$.
如图,在斜三棱柱 A BC-A1 B1C1中,侧面 ACC1 A1与侧面C B B1C1都是菱形,∠ACC1=∠CC1 B1=60°,AC=2,AB1=$\sqrt{6}$.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com