
���� ��������ͬ�����Ǻ���������ϵʽ��ȥ�����ȣ����ɵõ�ԲC�ı����̣�
������ȥ����t�õ�ֱ�߷��̣����Բ��Բ����뾶������Բ�ĵ�ֱ�ߵľ�����뾶�Ĺ�ϵ���г�����ʽ��⼴�ɣ�
��� �⣺����ԲC��$\left\{{\begin{array}{l}{x=1+\sqrt{2}cos��}\\{y=1-\sqrt{2}sin��}\end{array}}\right.$����Ϊ����������ȥ�ȿɵã���x-1��2+��y-1��2=2��
��x2+y2-2x-2y=0����2-2��cos��-2��sin��=0��
����$��=2\sqrt{2}sin����+\frac{��}{4}��$����5�֣�
����$��=\frac{��}{2}$ʱ��ֱ����Բû�й�����
��$����\frac{��}{2}$ʱ��ֱ�߷���Ϊy-1=tan����x+1����tan��•x-y+��tan��+1��=0
��ֱ����Բ�й�����ʱ��$\frac{|2tan��|}{{\sqrt{{{tan}^2}��+1}}}��\sqrt{2}$�����-1��tan����1
�ߦ���[0���У��������ȡֵ��Χ��$[0��\frac{��}{4}]��[\frac{3��}{4}���У�$�� ����10�֣�
���� ���⿼��Բ�IJ�����������ͨ���̵Ļ�������ͨ�����뼫���귽�̵Ļ���������㵽ֱ�ߵľ��빫ʽ��Ӧ�ã�


 ����ѧ��Ӧ�����ϵ�д�
����ѧ��Ӧ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
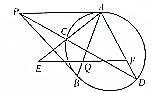 ��ͼ����Բ��һ��P��Բ����������PA��PB��A��BΪ�е㣬�ٹ�P����Բ��һ�����߷ֱ���Բ���ڵ�C��D����AB����һ��Q��PA��ƽ���߷ֱ���ֱ��AC��AD���ڵ�E��F��֤����QE=QF��
��ͼ����Բ��һ��P��Բ����������PA��PB��A��BΪ�е㣬�ٹ�P����Բ��һ�����߷ֱ���Բ���ڵ�C��D����AB����һ��Q��PA��ƽ���߷ֱ���ֱ��AC��AD���ڵ�E��F��֤����QE=QF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��֪����ͼ������P-ABCD�У�����ABCDΪ���Σ���BAD=60�㣬����PAD�͵���ABCD��PA=PD��
��֪����ͼ������P-ABCD�У�����ABCDΪ���Σ���BAD=60�㣬����PAD�͵���ABCD��PA=PD���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com