练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知函数f(x)＝x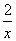－，g(x)＝a(2－ln x)(a>0)．若曲线y＝f(x)与曲线y＝g(x)在x＝1处的切线斜率相同，求a的值，并判断两条切线是否为同一条直线．


    解：根据题意有

    曲线y＝f(x)在x＝1处的切线斜率为

    f′(1)＝3，

    曲线y＝g(x)在x＝1处的切线斜率为

    g′(1)＝－a.

    所以f′(1)＝g′(1)，即a＝－3.

    曲线y＝f(x)在x＝1处的切线方程为y－f(1)＝3(x－1)，又f(1)＝－1，

    得：y＋1＝3(x－1)，即切线方程为3x－y－4＝0.

    曲线y＝g(x)在x＝1处的切线方程为y－g(1)＝3(x－1)．又g(1)＝－6.

    得y＋6＝3(x－1)，即切线方程为3x－y－9＝0，所以，两条切线不是同一条直线．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：


    已知函数y＝的图像与函数y＝kx－2的图像恰有两个交点，则实数k的取值范围是________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    [x]表示不超过x的最大整数，例如[2.9]＝2，[－4.1]＝－5，已知f(x)＝x－[x](x∈R)，g(x)＝log4(x－1)，则函数h(x)＝f(x)－g(x)的零点个数是(　　)

    A．1                                                   B．2

    C．3                                                   D．4

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    对于函数f(x)，如果存在锐角θ，使得f(x)的图像绕坐标原点逆时针旋转角θ，所得曲线仍是一函数，则称函数f(x)具备角θ的旋转性，下列函数具备角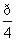的旋转性的是(　　)

    A．y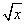＝             B．y＝ln x     C．y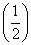＝x     D．y＝x2

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    若曲线y＝ax2－ln x在点(1，a)处的切线平行于x轴，则a＝________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    函数f(x)在定义域R内可导，若f(x)＝f(2－x)，且当x∈(－∞，1)时，(x－1)f′(x)<0，设a＝f(0)，b＝f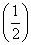，c＝f(3)，则(　　)

    A．a<b<c                                            B．c<b<a

    C．c<a<b                                            D．b<c<a

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知函数f(x)＝ax＋x2－xln a－b(a，b∈R，a>1)，e是自然对数的底数．

    (1)试判断函数f(x)在区间(0，＋∞)上的单调性；

    (2)当a＝e，b＝4时，求整数k的值，使得函数f(x)在区间(k，k＋1)上存在零点．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    电动自行车的耗电量y与速度x之间有关系y＝x3－x2－40x(x>0)，为使耗电量最小，则速度应定为________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：


    已知a>0，函数f(x)＝－2asin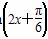＋2a＋b，当x∈时，－5≤f(x)≤1.

    (1)求常数a，b的值；

    (2)设g(x)＝且lg g(x)>0，求g(x)的单调区间．

    查看答案和解析>>

    同步练习册答案