
[x]表示不超过x的最大整数,例如[2.9]=2,[-4.1]=-5,已知f(x)=x-[x](x∈R),g(x)=log4(x-1),则函数h(x)=f(x)-g(x)的零点个数是( )
A.1 B.2
C.3 D.4
科目:高中数学 来源: 题型:
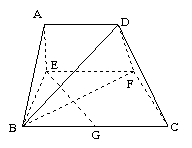
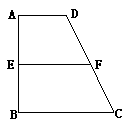
已知梯形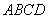 中,
中,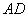 ∥
∥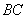 ,
,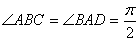 ,
, 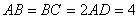 ,
,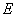 、
、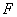 分别是
分别是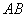 、
、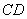 上的点,
上的点,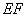 ∥
∥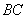 ,
,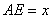 ,
, 是
是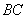 的中点.沿
的中点.沿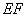 将梯形
将梯形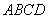 翻折,使平面
翻折,使平面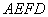 ⊥平面
⊥平面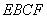 (如图) . (Ⅰ) 当
(如图) . (Ⅰ) 当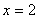 时,求证:
时,求证: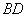 ⊥
⊥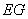 ;
;
(Ⅱ) 若以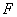 、
、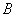 、
、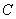 、
、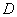 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为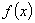 ,求
,求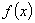 的最大值;
的最大值;
(Ⅲ)当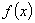 取得最大值时,求二面角
取得最大值时,求二面角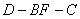 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
设f(x)与g(x)是定义在同一区间[a,b]上的两个函数,若函数y=f(x)-g(x)在x∈[a,b]上有两个不同的零点,则称f(x)和g(x)在[a,b]上是“关联函数”,区间[a,b]称为“关联区间”.若f(x)=x2-3x+4与g(x)=2x+m在[0,3]上是“关联函数”,则m的取值范围为________.
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=loga|x|在(0,+∞)上单调递增,则( )
A.f(3)<f(-2)<f(1) B.f(1)<f(-2)<f(3)
C.f(-2)<f(1)<f(3) D.f(3)<f(1)<f(-2)
查看答案和解析>>
科目:高中数学 来源: 题型:
某大楼共有12层,有11人在第1层上了电梯,他们分别要去第2至第12层,每层1人.因特殊原因,电梯只允许停1次,只可使1人如愿到达,其余10人都要步行到达所去的楼层.假设乘客每向下步行1层的“不满意度”增量为1,每向上步行1层的“不满意度”增量为2,10人的“不满意度”之和记为S.则S最小时,电梯所停的楼层是( )
A.7层 B.8层 C.9层 D.10层
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=x-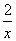 ,g(x)=a(2-ln x)(a>0).若曲线y=f(x)与曲线y=g(x)在x=1处的切线斜率相同,求a的值,并判断两条切线是否为同一条直线.
,g(x)=a(2-ln x)(a>0).若曲线y=f(x)与曲线y=g(x)在x=1处的切线斜率相同,求a的值,并判断两条切线是否为同一条直线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com