
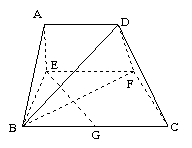
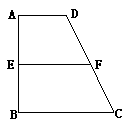
已知梯形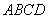 中,
中,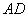 ∥
∥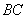 ,
,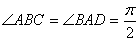 ,
, 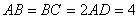 ,
,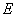 、
、 分别是
分别是 、
、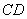 上的点,
上的点,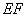 ∥
∥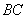 ,
,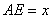 ,
, 是
是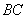 的中点.沿
的中点.沿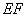 将梯形
将梯形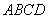 翻折,使平面
翻折,使平面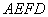 ⊥平面
⊥平面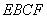 (如图) . (Ⅰ) 当
(如图) . (Ⅰ) 当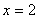 时,求证:
时,求证: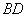 ⊥
⊥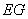 ;
;
(Ⅱ) 若以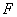 、
、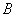 、
、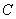 、
、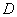 为顶点的三棱锥的体积记为
为顶点的三棱锥的体积记为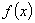 ,求
,求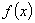 的最大值;
的最大值;
(Ⅲ)当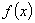 取得最大值时,求二面角
取得最大值时,求二面角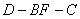 的余弦值.
的余弦值.
科目:高中数学 来源: 题型:
设集合M={x|0<x≤3},N={x|0<x≤2},那么“a∈M”是“a∈N”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
查看答案和解析>>
科目:高中数学 来源: 题型:
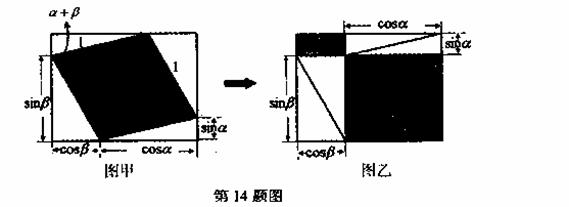
“无字证明”(proofs without words),就是将数学命题用简单、有创意而且易于理解的几何图形来呈现.请利用图甲、图乙中阴影部分的面积关系,写出该图所验证的一个三角恒等变换公式: .
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(x),g(x)分别是定义在R上的奇函数和偶函数,且f(x)-g(x)=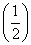 x,则f(1),g(0),g(-1)之间的大小关系是______________.
x,则f(1),g(0),g(-1)之间的大小关系是______________.
查看答案和解析>>
科目:高中数学 来源: 题型:
[x]表示不超过x的最大整数,例如[2.9]=2,[-4.1]=-5,已知f(x)=x-[x](x∈R),g(x)=log4(x-1),则函数h(x)=f(x)-g(x)的零点个数是( )
A.1 B.2
C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com