练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．“x≥1”是“lgx≥0”的（　　）
    A．充分不必要条件B．必要不充分条件
    C．充要条件D．既不充分也不必要条件

    分析 lgx≥0?x≥1．即可判断出结论．

    解答 解：lgx≥0?x≥1．
    ∴“x≥1”是“lgx≥0”的充要条件．
    故选：C．

    点评 本题考查了对数函数的单调性、简易逻辑的判定方法，考查了推理能力与计算能力，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

    9．已知向量$\overrightarrow{a}$=（5，m），$\overrightarrow{b}$=（2，-2）且（$\overrightarrow{a}$+$\overrightarrow{b}$）⊥$\overrightarrow{b}$，则m=（　　）
    A．-9B．9C．6D．-6

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知抛物线y2=4x的焦点为F，直线l过F且与抛物线交于A、B两点，若|AB|=5，则AB中点的横坐标为（　　）
    A．$\frac{5}{2}$B．2C．$\frac{3}{2}$D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    7．已知长方体ABCD-A1B1C1D1中，AB=BC，AA1=2AB，E为AA1中点，则异面直线BE与CD1所形成角的余弦值为（　　）
    A．$\frac{\sqrt{10}}{10}$B．$\frac{1}{5}$C．$\frac{3\sqrt{10}}{10}$D．$\frac{3}{5}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

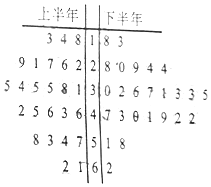    14．自贡某工厂于2016年下半年对生产工艺进行了改造（每半年为一个生产周期），从2016年一年的产品中用随机抽样的方法抽取了容量为50的样本，用茎叶图表示（如图）．已知每个生产周期内与其中位数误差在±5范围内（含±5）的产品为优质品，与中位数误差在±15范围内（含±15）的产品为合格品（不包括优质品），与中位数误差超过±15的产品为次品．企业生产一件优质品可获利润20元，生产一件合格品可获利润10元，生产一件次品要亏损10元
    （Ⅰ）求该企业2016年一年生产一件产品的利润为10的概率；
    （Ⅱ）是否有95%的把握认为“优质品与生产工艺改造有关”．
    附：
    P（K2≥k）0.0500.0100.001
    k3.8416.63510.828
    K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．已知$\overrightarrow{OA}$=（cos2x，-1），$\overrightarrow{OB}$=（1，sin2x+$\sqrt{3}$sin2x）（x∈R），若f（x）=$\overrightarrow{OA}$•$\overrightarrow{OB}$，则函数f（x）的最小值为（　　）
    A．-2B．0C．-$\sqrt{3}$D．-1

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    11．已知函数f（x）=lnx-x-3．
    （Ⅰ）求函数f（x）的最大值；
    （Ⅱ）求证：ln（22+1）+ln（32+1）+ln（42+1）+…ln（n2+1）＜1+2lnn!（n≥2，n∈N*）

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    16．已知圆F方程为（x-1）2+y2=1，圆外一点P到圆心的距离等于它到y轴距离，
    （1）求点P的轨迹方程．
    （2）直线l与点P轨迹方程交于y轴的右侧A，B不同两点，若$\overrightarrow{OA}$•$\overrightarrow{OB}$=-4（O为坐标原点），且4$\sqrt{6}$≤|$\overrightarrow{AB}$|≤4$\sqrt{30}$，求直线l的斜率k的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    17．定义运算$|{\begin{array}{l}a&b\\ c&d\end{array}}|=ad-bc$，若$|{\begin{array}{l}{sinθ}&2\\{cosθ}&3\end{array}}|=0$，则2sin2θ+sinθcosθ的值是$\frac{14}{13}$．

    查看答案和解析>>

    同步练习册答案