
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| ||
| 2 |
| 3 |
| ||
| 2 |
(
| ||
| a2 |
(
| ||||
| b2 |
| x2 |
| 4 |
| y2 |
| 3 |
| x2 |
| 4 |
| y2 |
| 3 |
| (2x+1)2 |
| 4 |
| (2y)2 |
| 3 |
| 1 |
| 2 |
| y2 | ||
|
| x02 |
| a2 |
| y02 |
| b2 |
| x2 |
| a2 |
| y2 |
| b2 |
| y-y0 |
| x-x0 |
| y+y0 |
| x+x0 |
| y-y0 |
| x-x0 |
| y+y0 |
| x+x0 |
| y2-y02 |
| x2-x02 |
| b2 |
| a2 |



| ƒÍº∂ | ∏þ÷–øŒ≥à | ƒÍº∂ | ≥ı÷–øŒ≥à |
| ∏þ“ª | ∏þ“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı“ª | ≥ı“ª√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ∂˛ | ∏þ∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı∂˛ | ≥ı∂˛√‚∑—øŒ≥ÃÕ∆ºˆ£° |
| ∏þ»˝ | ∏þ»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° | ≥ı»˝ | ≥ı»˝√‚∑—øŒ≥ÃÕ∆ºˆ£° |
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫Ω‚¥Ã‚
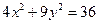 ±»Õ÷‘≤Ω𵄑⁄
±»Õ÷‘≤Ω𵄑⁄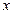 ÷·…œµƒÕ÷‘≤
÷·…œµƒÕ÷‘≤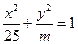 ∏¸Ω”Ω¸”⁄‘≤£¨«Û
∏¸Ω”Ω¸”⁄‘≤£¨«Û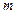 µƒ∑∂Œß°£
µƒ∑∂Œß°£≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫Ω‚¥Ã‚
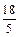 µƒæý¿Î÷Ʊ» «
µƒæý¿Î÷Ʊ» «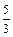 £¨‘Úµ„PµƒπϺ£∑Ω≥à «£® £©
£¨‘Úµ„PµƒπϺ£∑Ω≥à «£® £©A£Æ | B£Æ | C£Æ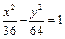 | D£Æ |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫µ•—°Ã‚
A£Æ
| B£Æ
| ||||||||
C£Æ
| D£Æ
|
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫µ•—°Ã‚
| A£ÆÕ÷‘≤ | B£ÆÀ´«˙œþ | C£Æ≈◊ŒÔœþ | D£Æ‘≤ |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫µ•—°Ã‚
A£Æ
| B£Æ
| C£Æ
| D£Æ
|
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫µ•—°Ã‚
| 6 |
A£Æ
| B£Æ
| C£Æ
| D£Æ
|
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫Ω‚¥Ã‚
| AC |
| BC |
| BC |
| AC |
| PQ |
| AB |
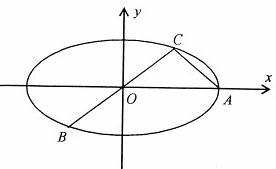
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
ø∆ƒø£∫∏þ÷– ˝—ß ¿¥‘¥£∫≤ªœÍ –գ∫µ•—°Ã‚
A£Æ
| ||||||||
B£Æ
| ||||||||
C£Æ
| ||||||||
| D£Æ“‘…œ∂º≤ª∂‘ |
≤Èø¥¥∞∏∫ÕΩ‚Œˆ>>
π˙º —ß–£”≈—° - ¡∑œ∞≤·¡–±Ì - ‘¡–±Ì
∫˛±± °ª•¡™Õ¯Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®∆Ωî | Õ¯…œ”–∫¶–≈œ¢æŸ±®◊®«¯ | µÁ–≈’©∆≠柱®◊®«¯ | …Ê¿˙ ∑–ÈŒÞ÷˜“”–∫¶–≈œ¢æŸ±®◊®«¯ | …Ê∆Û«÷»®æŸ±®◊®«¯
Œ•∑®∫Õ≤ª¡º–≈œ¢æŸ±®µÁª∞£∫027-86699610 柱®” œ‰£∫58377363@163.com