
分析 根据集合的基本定义,进行运算即可.
解答 解:A={x|-1≤x<3},B={x|1<x≤3},全集为R,
①A∩B={x|1<x<3}=(1,3),
A∪B={x|-1≤x≤3}=[-1,3];
②∁UA={x|x<-1或x≥3}=(-∞,-1)∪[3,+∞);
③∁U(A∪B)={x|x<-1或x>3}=(-∞,-1)∪(3,+∞);
④∁UB={x|x≤1或x>3}=(-∞,1]∪(3,+∞),
∴(∁UA)∩(∁UB)=(-∞,-1)∪(3,+∞).
故答案为:(1,3),[-1,3];(-∞,-1)∪[3,+∞);(-∞,-1)∪(3,+∞);(-∞,-1)∪(3,+∞).
点评 本题考查了集合的基本运算问题,是基础题目.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:高中数学 来源: 题型:选择题
| A. | ①② | B. | ③ | C. | ①③ | D. | ②③ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
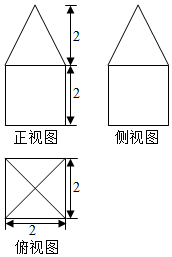
| A. | 8 cm3 | B. | 12 cm3 | C. | $\frac{32}{3}$ cm3 | D. | $\frac{40}{3}$ cm3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,+∞) | B. | (1,+∞) | C. | (1,2) | D. | $({1,\frac{4}{3}})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com