
分析 (1)根据幂函数的性质,结合题意得-k2+k+2>0,从而求出k的值;
(2)由k的值得出f(x)=x2,写出g(x)的解析式,配方后讨论对称轴的范围,从而求出g(x)的最值,得出值域,即可求出对应的p.
解答 解:(1)由f(2)<f(3),得-k2+k+2>0,
即k2-k-2<0,
又k∈Z,
解得k=0或1;
(2)k=0或1时,f(x)=x2,
g(x)=1-pf(x)+(2p-1)x=-p${(x-\frac{2p-1}{2p})}^{2}$+$\frac{{4p}^{2}+1}{4p}$,
当$\frac{2p-1}{2p}∈[-1,2]$,即$p∈[\frac{1}{4},+∞)$时,$\frac{{4{p^2}+1}}{4p}=\frac{17}{8}$,
解得p=2,g(-1)=-4,g(2)=-1;
当$\frac{2p-1}{2p}∈(2,+∞)$时,∵p>0,∴这样的p不存在;
当$\frac{2p-1}{2p}∈(-∞,-1)$,即$p∈(0,\frac{1}{4})$时,$g(-1)=\frac{17}{8},g(2)=-4$,这样的p不存在;
综上得,p=2.
点评 本题考查了幂函数的定义与性质的应用问题,也考查了分类讨论思想的应用问题,是综合性题目.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2π | B. | π | C. | $\frac{4π}{3}$ | D. | $\frac{5π}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=2sinx | B. | f(x)=2cosx | C. | f(x)=cos2x | D. | f(x)=sin2x |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2x | B. | -3x | C. | -3 | D. | -2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
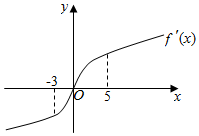
| A. | (-3,0) | B. | (-3,5) | C. | (0,5) | D. | (-∞,-3)∪(5,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com