
给出下列命题:
① 存在实数 ,使
,使 ;
;
② 若 、
、 是第一象限角,且
是第一象限角,且 >
> ,则cos
,则cos <cos
<cos ;
;
③ 函数 是偶函数;
是偶函数;
④ A、B、C为锐角 的三个内角,则
的三个内角,则
其中正确命题的序号是____________.(把正确命题的序号都填上)
科目:高中数学 来源: 题型:填空题
下列命题中,真命题的序号为 .
(1)在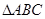 中,若
中,若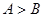 ,则
,则 ;
;
(2)已知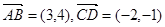 ,则
,则 在
在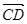 上的投影为
上的投影为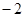 ;
;
(3)已知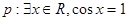 ,
,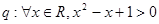 ,则“
,则“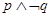 ”为假命题;
”为假命题;
(4)要得到函数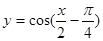 的图象,只需将
的图象,只需将 的图象向左平移
的图象向左平移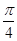 个单位.
个单位.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列命题:①动点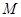 到两定点
到两定点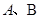 的距离之比为常数
的距离之比为常数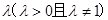 ,则动点
,则动点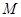 的轨迹是圆;②椭圆
的轨迹是圆;②椭圆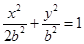 的离心率是
的离心率是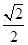 ;③双曲线
;③双曲线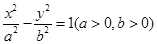 的焦点到渐近线的距离是b;④已知抛物线
的焦点到渐近线的距离是b;④已知抛物线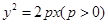 上两点
上两点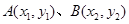 ,且OA⊥OB (O是坐标原点),则
,且OA⊥OB (O是坐标原点),则 .所有正确命题的序号是_______________.
.所有正确命题的序号是_______________.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
下列命题中_________为真命题.
① “A∩B=A”成立的必要条件是“A B”,
B”,
②“若x2+y2=0,则x,y全为0”的否命题,
③“全等三角形是相似三角形”的逆命题,
④“圆内接四边形对角互补”的逆否命题。
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
已知函数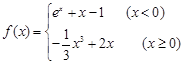 ,给出如下四个命题:
,给出如下四个命题:
① 在
在 上是减函数;②
上是减函数;② 的最大值是2;
的最大值是2;
③函数 有两个零点;④
有两个零点;④ 在R上恒成立.
在R上恒成立.
其中正确的命题有 .(把正确的命题序号都填上).
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
在下列结论中:
①若不等式 的解集为
的解集为 ,则
,则 ;
;
②命题 ,若
,若 ,则
,则 或
或 的否命题是假命题;
的否命题是假命题;
③在 中,
中, 的充要条件是
的充要条件是 ;
;
④若非零向量 两两成的夹角均相等,则夹角的大小为
两两成的夹角均相等,则夹角的大小为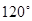 ;
;
其中正确命题的序号是 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com